
Квадра́т — правильный четырёхугольник, то есть плоский четырёхугольник, у которого все углы и все стороны равны. Каждый угол квадрата — прямой  .
.

Окта́эдр — многогранник с восемью гранями.

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Мозаика Пенроуза — общее название трёх особых типов непериодического разбиения плоскости; названы по имени английского математика Роджера Пенроуза, исследовавшего их в 1970-е годы.

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.

Квадра́тный парке́т, квадратный паркетаж, квадратная мозаика или квадратная решётка — это замощение плоскости равными квадратами, расположенными сторона к стороне, при этом вершины четырёх смежных квадратов находятся в одной точке. Символ Шлефли мозаики — {4,4}, означающий, что вокруг каждой вершины имеется 4 квадрата.

Треуго́льный парке́т или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.

Шестиуго́льный парке́т или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.

Усечение — операция в пространстве любой размерности, которая отсекает вершины многогранника и при которой образуются новые грани на месте вершин. Термин берёт начало от названий архимедовых тел, данных Кеплером.
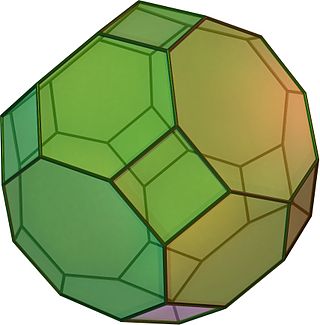
Усечённый кубооктаэдр, усечённый кубоктаэдр — полуправильный многогранник с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию, усечённый кубооктаэдр является зоноэдром.

Ромбическая мозаика, кантующиеся блоки, обратимые кубы или кубическая решётка — мозаика одинаковых ромбов с углом 60° на евклидовой плоскости. Каждый ромб имеет два угла 60° и два 120°. Такие ромбы иногда называют диамондами. Множества из трёх ромбов соприкасаются вершинами с углом 120°, а множества из шести — вершинами с углом 60°.

Пифагорова мозаика — замощение евклидовой плоскости квадратами двух различных размеров, в которой каждый квадрат касается четырёх квадратов другого размера своими четырьмя сторонами. Исходя из этой мозаики, можно доказать (наглядно) теорему Пифагора, за что мозаика и получила название пифагоровой. Мозаика часто используется в качестве узора для кафельного пола. В этом контексте мозаика известна также как узор классов.
Однородная мозаика — вершинно транзитивная мозаика на плоскости с правильными многоугольными гранями.

Усечённая квадратная мозаика — полуправильная мозаика из правильных многоугольников на евклидовой плоскости с одним квадратом и двумя восьмиугольниками в каждой вершине. Это единственная мозаика из правильных выпуклых многоугольников, содержащая соприкасающиеся сторонами восьмиугольники. Символ Шлефли мозаики равен t{4,4}.

Тришестиугольная мозаика — одна из 11 однородных мозаик на евклидовой плоскости из правильных многоугольников. Мозаика состоит из правильных треугольников и правильных шестиугольников, расположенных так, что каждый шестиугольник окружён треугольниками, и наоборот. Название мозаики вызвано тем фактом, что она комбинирует правильную шестиугольную мозаику и правильную треугольную мозаику. Два шестиугольника и два треугольника чередуются вокруг каждой вершины, а рёбра образуют бесконечную конфигурацию прямых. Двойственная мозаика — ромбическая.

Нотация Конвея для многогранников, разработанная Конвеем и продвигаемая Хартом, используется для описания многогранников, опираясь на затравочный многогранник, модифицируемый различными префикс-операциями.

Разделённая квадратная мозаика (или тетракис-квадратная мозаика — это мозаика в евклидовой плоскости, которая строится из квадратной мозаики путём деления каждого квадрата на четыре равнобедренных прямоугольных треугольника с вершинами в центрах квадратов, в результате чего образуется бесконечная конфигурация прямых. Мозаика может быть также построена путём деления каждого квадрата решётки на два треугольника диагональю, при этом диагонали соседних квадратов имеют различное направление. Мозаику можно получить также путём наложения двух квадратных мозаик, одна из которых повёрнута на 45 градусов и её масштаб увеличен на √2.

Фаска или усечение рёбер в геометрии — это топологическая операция, которая преобразует многогранник в другой многогранник. Операция подобна растяжению, передвигающему грани, удаляя их от центра. Для трёхмерных многогранников операция фаски добавляет новую шестиугольную грань вместо каждого исходного ребра.

Группа орнамента — это математическая классификация двумерных повторяющихся узоров, основанных на симметриях. Такие узоры часто встречаются в архитектуре и декоративном искусстве. Существует 17 возможных различных групп.









































