Квадратный корень из 3

Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — e^π и π
Система счисления	Оценка числа √3
Десятичная	1,7320508075688772935…
Двоичная	1,1011101101100111101…
Шестнадцатеричная	1,BB67AE8584CAA73B…
Шестидесятеричная	1; 43 55 22 58 27 57 56 …
Рациональные приближения	⁵/₃; ⁷/₄; ¹⁹/₁₁; ²⁶/₁₅^[1]; ⁷¹/₄₁; ⁹⁷/₅₆; ²⁶⁵/₁₅₃^[1]; ³⁶²/₂₀₉; ⁹⁸⁹/₅₇₁; ¹³⁵¹/₇₈₀^[1] (перечислено в порядке увеличения точности)
Непрерывная дробь	$1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+\ddots }}}}}}}}}}$

Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3. Обозначение: ${\sqrt {3}}.$

Значение

Квадратный корень из 3 является иррациональным числом, то есть не может быть точно представлен никакой конечной дробью. С точностью до 0,01 % значение ${\sqrt {3}}\approx 1{,}732.$ Хорошее приближение даёт также обыкновенная дробь ${\tfrac {97}{56}}\approx 1{,}73214.$

Может быть также выражен:

непрерывной дробью [1; 1, 2, 1, 2, 1, 2, …];
бесконечным вложенным радикалом:

{\sqrt {3}}=-1+2{\sqrt {{\frac {1}{2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {{\frac {1}{2}}+...}}}}}}.

Применение

Геометрия и тригонометрия

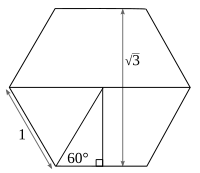
Если длина стороны равностороннего треугольника равна 1, то каждая высота этого треугольника равна ${\sqrt {3}}/2.$

${\sqrt {3}}$ равен также:

тангенсу 60°;
расстоянию между параллельными сторонами правильного шестиугольника со сторонами 1;
длине диагонали куба со стороной 1;
длине стороны равностороннего треугольника, у которого радиус описанной окружности равен 1.

Электроэнергетика

При трёхфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в ${\sqrt {3}}$ больше модуля фазного напряжения.

См. также

Литература

Выгодский М. Я. Справочник по элементарной математике. — Изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
Щетников А. И. К вопросу о рациональных приближениях ${\sqrt {3}}$ у Архимеда: новая реконструкция. — Труды вторых Колмогоровских чтений. — Ярославль: Изд. ЯГПУ, 2004. — С. 136—144. — 382 с.

Примечания

↑ ¹ ² ³ Эти приближения были известны Архимеду
↑ The square root of three (неопр.). Дата обращения: 15 февраля 2015. Архивировано 4 февраля 2015 года.

Ссылки

Proof that square root of 3 is irrational (англ.)
Weisstein, Eric W. Theodorus' Constant (англ.) на сайте Wolfram MathWorld.

Иррациональные числа
Постоянная Апери (ζ(3)) Константа Эрдёша — Борвейна (E) Постоянные Фейгенбаума Мечта софомора Константа простых чисел (ρ) Пластическое число (ρ) Логарифм двойки (ln 2) Корень 12-й степени из 2^[англ.] (¹²√2) Квадратный корень из 2 (√2) Квадратный корень из 3 (√3) Квадратный корень из 5 (√5) Золотое сечение (φ) Сверхзолотое сечение (ψ) Серебряное сечение (δ_S) e π Постоянная Гельфонда (e^π) Постоянная Гельфонда — Шнайдера (2^√2) Обратная постоянная Фибоначчи (ψ)
Трансцендентные Тригонометрические Шизофренические

Похожие исследовательские статьи

Квадрату́ра кру́га — задача, заключающаяся в нахождении способа построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу. Наряду с трисекцией угла и удвоением куба, является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.

<span class="mw-page-title-main">Октаэдр</span> многогранник, имеющий 8 граней

Окта́эдр — многогранник с восемью гранями.

Квадра́тный ко́рень из числа $\text{[math]}$ — число $\text{[math]}$ , дающее $\text{[math]}$ при возведении в квадрат: $\text{[math]}$ Равносильное определение: квадратный корень из числа $\text{[math]}$ — решение уравнения $\text{[math]}$ Операция вычисления значения квадратного корня из числа $\text{[math]}$ называется «извлечением квадратного корня» из этого числа.

<span class="mw-page-title-main">Правильный тетраэдр</span> тело Платона

Тетраэдр называется правильным, если все его грани — равносторонние треугольники.

Сере́бряное сече́ние — математическая константа, выражающая некоторое геометрическое соотношение, выделяемое эстетически. В отличие от золотого сечения, по аллюзии с которым оно названо, серебряное сечение не имеет единого определения, наиболее последовательным является следующее:

<span class="mw-page-title-main">Быстрый обратный квадратный корень</span> быстрый приближённый алгоритм вычисления обратного квадратного корня

Бы́стрый обра́тный квадра́тный ко́рень или 0x5F3759DF по используемой «магической» константе) — это приближённый алгоритм вычисления обратного квадратного корня $\text{[math]}$ для положительных 32-битных чисел с плавающей запятой. Алгоритм использует целочисленные операции «вычесть» и «битовый сдвиг», а также дробные «вычесть» и «умножить» — без медленных операций «разделить» и «квадратный корень». Несмотря на «хакерство» на битовом уровне, приближение монотонно и непрерывно: близкие аргументы дают близкий результат. Точности не хватает для настоящих численных расчётов и даже для нормирования матриц поворота в трёхмерной графике, однако вполне достаточно для маловажных эффектов вроде освещения и теней.

Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: $\text{[math]}$

Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.

<span class="mw-page-title-main">Ромбоикосододекаэдр</span> полуправильный многогранник, состоящий из 12 правильных пятиугольников, 30 квадратов и 20 треугольников

Ромбоикосододека́эдр — полуправильный многогранник с 62 гранями, составленный из 20 правильных треугольников, 30 квадратов и 12 правильных пятиугольников.

<span class="mw-page-title-main">Дельтоидальный гексеконтаэдр</span> полуправильный многогранник (каталаново тело), двойственный ромбоикосододекаэдру

Дельтоида́льный гексеконта́эдр — полуправильный многогранник, двойственный ромбоикосододекаэдру. Составлен из 60 одинаковых выпуклых дельтоидов.

<span class="mw-page-title-main">Гекзакисоктаэдр</span> полуправильный многогранник (каталаново тело), двойственный ромбоусечённому кубооктаэдру

Гекзакисокта́эдр, также называемый дисдакисдодека́эдром, — полуправильный многогранник, двойственный ромбоусечённому кубооктаэдру.

<span class="mw-page-title-main">Пентагональный гексеконтаэдр</span> полуправильный многогранник (каталаново тело), двойственный курносому додекаэдру

Пентагона́льный гексеконта́эдр — полуправильный многогранник, двойственный курносому додекаэдру. Составлен из 60 одинаковых неправильных пятиугольников.

<span class="mw-page-title-main">Клинокорона</span>

Клинокоро́на — один из многогранников Джонсона.

Уплощённая треуго́льная клинорото́нда — один из многогранников Джонсона.

Плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней. Многогранник является двенадцатигранником, одним из восьми дельтаэдров и одним из 92 многогранников Джонсона.

Спираль Феодора — приближение к архимедовой спирали, состоящее из смежных прямоугольных треугольников, примыкающих друг к другу. Она названа в честь Феодора Киренского, древнегреческого ученого, известного как учитель Платона, жившего в V веке до нашей эры на территории Ливии.

Два́жды ко́со отсечённый ромбоикосододека́эдр — один из многогранников Джонсона.

<span class="mw-page-title-main">Равнобедренный прямоугольный треугольник</span> треугольник, в котором один угол равен 90 градусов и две стороны равны между собой

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый внутренний угол равен 45°:

\text{[math]}

<span class="mw-page-title-main">Опоясанный двуклинник</span>

Опоя́санный двукли́нник — один из многогранников Джонсона.

Методы вычисления квадратных корней — это вычислительные алгоритмы для вычисления приближённых значений главных квадратных корней вещественного числа. Арифметически это означает, что если дано число $\text{[math]}$ , процедура находит число, которое при умножении на себя даёт $\text{[math]}$ . Алгебраически это означает процедуру нахождения неотрицательного корня уравнения $\text{[math]}$ . Геометрически это означает построение стороны квадрата с заданной площадью.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.