Квантование (обработка сигналов)

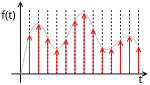
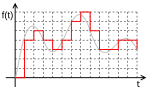
Квантова́ние (англ. quantization) — в обработке сигналов — разбиение диапазона отсчётных значений сигнала на конечное число уровней и округление этих значений до одного из двух ближайших к ним уровней[1]. При этом значение сигнала может округляться либо до ближайшего уровня, либо до меньшего или большего из ближайших уровней в зависимости от способа кодирования[2]. Такое квантование называется скалярным. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей и замена этих значений идентификатором одной из этих областей[3].
Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике — по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (на графике — по вертикали). В АЦП округление может производиться до ближайшего меньшего уровня. Сигнал, к которому применены дискретизация и квантование, называется цифровым.
Квантование часто используется при обработке сигналов, в том числе при сжатии звука и изображений.
При оцифровке сигнала количество битов, кодирующих один уровень квантования, называют глубиной квантования или разрядностью. Чем больше глубина квантования и чем больше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае равномерного квантования глубина квантования определяет динамический диапазон, измеряемый в децибелах (1 бит на 6 дБ)[4].
Виды квантования
Равномерное (однородное) квантование — разбиение диапазона значений отсчётов сигнала на отрезки равной длины и замена этих значений на ближайший уровень квантования . В этом случае возможны два варианта квантования[5]:
1. Если значения сигнала находятся в интервале , где — шаг квантования, то они округляются до уровня (midrise — характеристика квантования с нулём на границе шага квантования):
2. Если значения сигнала находятся в интервале , то они округляются до нулевого уровня (midtread — характеристика квантования с нулём в центре шага квантования):
- ,
где — округление до ближайшего меньшего целого.
После дискретизации и квантования получается цифровой сигнал. Затем уровень квантования заменяется набором чисел. Для квантования в двоичном коде диапазон изменения сигнала от минимального значения до максимального значения делится на уровней квантования, где — разрядность квантования. Величина получившегося интервала между уровнями (шаг квантования):
Каждому уровню присваивается -разрядный двоичный код — номер уровня, записанный двоичным числом. Каждому отсчёту сигнала присваивается код ближайшего к нему уровню. Таким образом, после дискретизации и квантования аналоговый сигнал представляется последовательностью двоичных чисел, соответствующих значениям сигнала в определённые моменты времени, то есть двоичным сигналом. При этом каждое двоичное число представляется последовательностью импульсов высокого (1) и низкого (0) уровня. Разрядность квантования звука обычно выбирается равной от 8 до 32 битов (сравнение цифровых аудиоформатов), но обычно 16 или 24 бита[6].
Неравномерное квантование — квантование, при котором разбиение диапазона значений сигнала производится на отрезки неравной длины. Применяется с целью повышения точности квантования в случае, когда распределение значений сигнала неравномерное, например при квантовании звука. При этом уровни квантования должны располагаться чаще в тех областях, где значения сигнала более вероятны. При квантовании речевых сигналов чаще используется компрессор, увеличивающий малые значения сигнала и уменьшающий большие значения, и последующее равномерное квантование.
Методы квантования
- Импульсно-кодовая модуляция
- Дельта-модуляция
- Сигма-дельта модуляция
Примечания
- ↑ Солонина А. И. Алгоритмы и процессоры цифровой обработки сигналов. — C. 8. Дата обращения: 12 марта 2018. Архивировано 13 марта 2018 года.
- ↑ Солонина А. И. Основы цифровой обработки сигналов: Курс лекций. 2 изд. — 2012. — C. 299. Дата обращения: 12 марта 2018. Архивировано 13 марта 2018 года.
- ↑ Pramod Jain. A Vector Quantization Multistart Method for Global Optimization. — University of California, 1989. — P. 37.
- ↑ Смирнов С. В. Средства и системы технического обеспечения обработки, хранения и передачи информации. — МГИУ, 2011. — С. 260. Дата обращения: 13 марта 2018. Архивировано 14 марта 2018 года.
- ↑ William A. Pearlman,Amir Said. Digital Signal Compression: Principles and Practice. — Cambridge University Press, 2011. — P. 83. Дата обращения: 26 марта 2018. Архивировано 27 марта 2018 года.
- ↑ Питер Кирн. Цифровой звук. Реальный мир. — 2008. — С. 65. Дата обращения: 19 марта 2018. Архивировано 19 марта 2018 года.


![{\displaystyle [0,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbede90a8f7ff59267c875f09e715c896ce7a51a)



![{\displaystyle [-h/2,h/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922227192ceb39da984dea7332cfb54ca07f36e1)
























