Мезоскопи́ческая фи́зика — раздел физики конденсированных сред, в котором рассматриваются свойства систем на масштабах промежуточных между макроскопическим и микроскопическим. Термин ввёл в 1981 году датский физик Ван Кампен. Многие законы, полученные в макроскопической физике, неприменимы в области мезоскопических размеров, например последовательно соединённые сопротивления нельзя вычислить суммированием отдельных сопротивлений, а следует учитывать квантовые эффекты. Именно мезоскопические размеры накладывают ограничения на классический транспорт в полупроводниках. Мезоскопика возникла в 80-х годах XX века как ответ на технологический прогресс микро- и нанолитографии, роста монокристаллов, а также инструментов типа сканирующего туннельного микроскопа, позволяющего проводить измерения на атомарном уровне.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму.
Магнитосопротивление — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнитосопротивлением. Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает этот эффект и вещество переходит в нормальное состояние, в котором наблюдается сопротивление. В нормальных металлах эффект магнитосопротивления выражен слабее. В полупроводниках относительное изменение сопротивления может быть в 100—10 000 раз больше, чем в металлах.
Эффект Шубникова — де Хааза назван в честь советского физика Л. В. Шубникова и нидерландского физика В. де Хааза, открывших его в 1930 году. Наблюдаемый эффект заключался в осцилляциях магнетосопротивления плёнок висмута при низких температурах. Позже эффект Шубникова — де Гааза наблюдали в многих других металлах и полупроводниках. Эффект Шубникова — де Гааза используется для определения тензора эффективной массы и формы поверхности Ферми в металлах и полупроводниках.
Те́нзор эне́ргии-и́мпульса (ТЭИ) — симметричный тензор второго ранга (валентности), описывающий плотность и поток энергии и импульса полей материи и определяющий взаимодействие этих полей с гравитационным полем.
Сла́бая локализа́ция — совокупность явлений, обусловленных эффектом квантово-механической интерференции электронов самих с собой в слабо разупорядоченных материалах с металлическим типом проводимости. Явления слабой локализации являются универсальными и проявляются в любых неупорядоченных проводниках — в металлическом стекле, тонких металлических плёнках, системах с двумерным электронным газом и других мезоскопических системах.
Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число.

В современной физике электромагни́тный потенциа́л обычно означает четырёхмерный потенциал электромагнитного поля, являющийся 4-вектором (1-формой). Именно в связи с векторным (4-векторным) характером электромагнитного потенциала электромагнитное поле относится к классу векторных полей в том смысле, который употребляется в современной физике по отношению к фундаментальным бозонным полям.
- Обозначается электромагнитный потенциал чаще всего
 или
или  , что подразумевает величину с индексом, имеющую четыре компоненты
, что подразумевает величину с индексом, имеющую четыре компоненты  или
или  , причём индексом 0, как правило, обозначается временная компонента, а индексами 1, 2, 3 — три пространственных. В данной статье мы будем придерживаться первого обозначения.
, причём индексом 0, как правило, обозначается временная компонента, а индексами 1, 2, 3 — три пространственных. В данной статье мы будем придерживаться первого обозначения. - В современной литературе могут использоваться более абстрактные обозначения.
Задача Кеплера вообще представляет собой проблему отыскания движения двух сферически-симметричных тел, взаимодействующих гравитационно. В классической теории тяготения решение этой проблемы было найдено самим Исааком Ньютоном: оказалось, что тела будут двигаться по коническим сечениям, в зависимости от начальных условий — по эллипсам, параболам или гиперболам. В рамках общей теории относительности (ОТО) с пуристической точки зрения эта задача представляется плохо поставленной, так как модель абсолютно твёрдого тела невозможна в релятивистской физике, а не абсолютно твёрдые тела не будут при взаимодействии сферически-симметричными. Другой подход включает переход к точечным телам, правомерный в ньютоновской физике, но вызывающий проблемы в ОТО. Помимо этого, кроме положений и скоростей тел необходимо задать также и начальное гравитационное поле (метрику) во всём пространстве — проблема начальных условий в ОТО. В силу указанных причин точного аналитического решения задачи Кеплера в ОТО не существует, но есть комплекс методов, позволяющих рассчитать поведение тел в рамках данной задачи с необходимой точностью: приближение пробного тела, постньютоновский формализм, численная относительность.
Конста́нта равнове́сия — величина, определяющая для данной химической реакции соотношение между термодинамическими активностями исходных веществ и продуктов в состоянии химического равновесия. Зная константу равновесия реакции, можно рассчитать равновесный состав реагирующей смеси, предельный выход продуктов, определить направление протекания реакции.

В физике элементарных частиц майора́новский фермио́н, или фермио́н Майора́ны — фермион, который является своей собственной античастицей. Существование таких частиц было впервые рассмотрено итальянским физиком Этторе Майораной в 1937 году. В экспериментах с полупроводниковыми нанопроволоками наблюдались квазичастицы, обладающие свойствами майорановского фермиона. Экспериментальное обнаружение майорановских частиц как в физике высоких энергий, так и в области физики твёрдого тела приведёт к важным последствиям для науки в целом.
Уравне́ния Шви́нгера — система уравнений, связывающих функции Грина в квантовой теории поля. Предложена Джулианом Швингером в 1951 году.
Пропагатор в квантовой механике и квантовой теории поля (КТП) — функция, характеризующая распространение релятивистского поля от одного акта взаимодействия до другого. Эта функция определяет амплитуду вероятности перемещения частицы из одного места пространства в другое за заданный промежуток времени или перемещения частицы с определённой энергией и импульсом. Для расчёта частоты столкновений в КТП используются виртуальные частицы, представленные в диаграммах Фейнмана пропагаторами, вносят свой вклад в вероятность рассеяния, описываемого соответствующей диаграммой. Их также можно рассматривать как оператор, обратный волновому оператору, соответствующему частице, и поэтому их часто называют (причинными) функциями Грина.
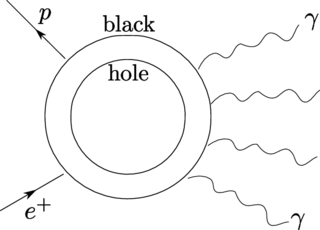
Виртуальная чёрная дыра — гипотетический объект квантовой гравитации: чёрная дыра, возникшая в результате квантовой флуктуации пространства-времени. Является одним из примеров так называемой квантовой пены и гравитационным аналогом виртуальных электрон-позитронных пар в квантовой электродинамике.
Температурные функции Грина являются некоторой модификацией функций Грина для квантовомеханических систем с температурой отличной от нуля. Они удобны для вычисления термодинамических свойств системы, а также содержат информацию о спектре квазичастиц и о слабонеравновесных кинетических явлениях.
Уравне́ние Шви́нгера — Томона́ги, в квантовой теории поля, основное уравнение движения, обобщающее уравнение Шрёдингера на релятивистский случай.
Ме́тод Га́усса в небесной механике и астродинамике используется для первоначального определения параметров орбиты небесного тела по трём наблюдениям.
В теории многих тел термин функция Грина иногда используется как синоним корреляционной функции, но относится к корреляторам операторов поля или операторам рождения и уничтожения.



































