В криптографии линейным криптоанализом называется метод криптоанализа, использующий линейные приближения для описания работы шифра.

Mathematische Annalen — германский математический журнал, издаваемый Springer Science+Business Media. Основан в 1868 году Альфредом Клебшем и Карлом Нейманом.

Треугольник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.

Поверхность Гурвица — компактная риманова поверхность, имеющая в точности
- 84(g − 1)
Поверхность Макбита, кривая Макбита или кривая Фрикке — Макбита, — это поверхность Гурвица рода 7.
Конец топологического пространства — грубо говоря, компонента связности его «идеальной границы». То есть, каждый конец представляет собой способ двигаться к бесконечности в пространстве.
Задача Бернштейна — задача о графике функции, являющимся минимальной поверхностью. Названа в честь Сергея Натановича Бернштейна, решившего 2-мерный случай этой задачи в 1914 году.

Людвиг Отто Блюменталь — немецкий математик, профессор Рейнско-Вестфальского технического университета Ахена. Был студентом Давида Гильберта и редактором журнала Mathematische Annalen.
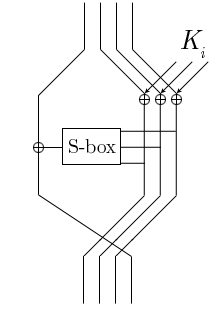
В криптографии, MacGuffin — симметричный блочный шифр, построенный на основе сети Фейстеля.

Бирациональная геометрия — это раздел алгебраической геометрии, основной задачей которого является классификация алгебраических многообразий с точностью до бирациональной эквивалентности. Это сводится к изучению отображений, которые задаются рациональными функциями, а не многочленами. Отображение может быть не определено в некоторых точках, являющихся полюсами рациональной функции.
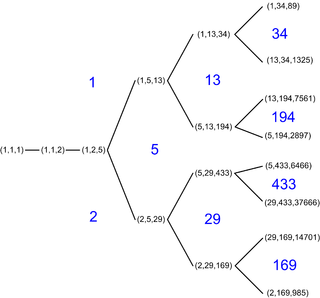
Числа Маркова — это положительные числа x, y или z, являющиеся решениями диофантова уравнения Маркова

Верхняя вена таламуса, ранее описанная в 1976 году Бенно Шлезингером как главная вена таламуса или основная вена таламуса или как центромедиальная вена таламуса, а Пироговым как внутренняя вена таламуса, является самой большой по калибру и самой важной из вен таламуса. Она собирает кровь от латеральных, вентральных и ретикулярной групп ядер таламуса, а также от ядер гипоталамуса, и впадает во внутреннюю мозговую вену. Она подвержена значительным межиндивидуальным анатомическим различиям и вариациям.

Фе́ликс Бернште́йн — немецкий математик. Первым доказал центральную для теории множеств теорему Кантора — Бернштейна. Определил также статистические законы наследования групп крови. Профессор Колумбийского, Сиракузского и Нью-Йоркского университетов.
Конфигурация Клейна — конфигурация, связанная с поверхностью Куммера, состоящей из 60 точек и 60 плоскостей, в которой каждая точка лежит на 15 плоскостях, а каждая плоскость проходит через 15 точек. Конфигурация использует 15 пар прямых 12. 13. 14. 15. 16. 23. 24. 25. 26. 34. 35. 36. 45. 46. 56 и их обратные. Ниже показаны 60 точек, полученные из троек пересекающихся прямых, образующих нечётные перестановки. Шестьдесят плоскостей — это тройки прямых, лежащих в одной плоскости и образующих чётные перестановки, полученные перестановкой последних двух цифр в точках. Для любой точки или плоскости существует 15 членов в другом множестве, содержащем эти 3 прямые.
Комплекс прямых — это трёхмерное алгебраическое многообразие, заданное как пересечение грассманиана G(2, 4) с гиперповерхностью. Оно называется комплексом прямых, так как точки G(2, 4) соответствуют прямым в P3, так что комплекс прямых можно понимать как трёхмерное семейство прямых в P3. Прямые этого семейства, проходящие через фиксированную точку, образуют конус, степень которого равна степени гиперповерхности, задающей комплекс. Линейный комплекс прямых и квадратичный комплекс прямых — это случаи, когда гиперповерхность имеет степень 1 или 2, в этих случаях комплекс прямых является рациональным многообразием.
Дедекиндова группа — это группа, всякая подгруппа которой нормальна.
Нормальные координаты — локальная система координат в окрестности точки риманова многообразия полученная из координат на касательном пространстве в данной точке применением экспоненциального отображения.
Теорема Бернштейна о седловом графике — классическая теорема о седловых поверхностях. Доказана Сергеем Натановичем Бернштейном.
Многочлен Боллобаша — Риордана — это инвариантный многочлен графов на ориентируемых поверхностях от трех переменных или инвариант ленточных графов от четырех переменных, обобщающий многочлен Татта.













