Кинетическая энергия

Виды энергии:
	Механическая	Потенциальная  Кинетическая
‹♦›	Внутренняя
	Электромагнитная	Электрическая  Магнитная
	Химическая
	Ядерная
${\displaystyle G}$	Гравитационная
${\displaystyle \emptyset }$	Вакуума
Гипотетические:
${\displaystyle }$	Тёмная
См. также: Закон сохранения энергии

Кинети́ческая эне́ргия — скалярная физическая величина, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

${\displaystyle E_{\mathrm {kin} }=\sum {{m_{i}v_{i}^{2}} \over 2},}$

где индекс ${\displaystyle \ i}$ нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[3]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[4]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: ${\displaystyle T}$, ${\displaystyle E_{\mathrm {kin} }}$, ${\displaystyle K}$ и другие. В системе СИ она измеряется в джоулях (Дж), в СГС — в эргах.

Упрощённо, кинетическая энергия — это работа, которую необходимо совершить, чтобы тело массой ${\displaystyle m}$ разогнать из состояния покоя до скорости ${\displaystyle v}$. Либо, наоборот, это работа, которую может совершить, останавливаясь, тело массой ${\displaystyle m}$, обладающее начальной скоростью ${\displaystyle v}$.

Прилагательное «кинетический» происходит от греческого слова κίνησις (kinesis, «движение»). Дихотомия между кинетической энергией и потенциальной энергией восходит к аристотелевским концепциям потенциальности и актуальности^{[англ.][5]} .

Лейбниц в своих трактатах 1686 и 1695 годов ввёл понятие «живой силы» (лат. vis viva), которую он определил как произведение массы объекта и квадрата его скорости (в современной терминологии — кинетическая энергия, только удвоенная)^[6].

Вильгельм Гравезанд из Нидерландов предоставил экспериментальные доказательства важности величины mv². Cбрасывая грузы с разной высоты на глиняный блок, он определил, что глубина их проникновения пропорциональна квадрату скорости удара. Эмили дю Шатле осознала значение данного эксперимента и опубликовала объяснение в книге «Учебник физики» (фр. Institutions de Physique, 1740)^[7].

Иоганн Бернулли использовал понятие "живой силы" для расчётов (в частности, движения идеальной жидкости). В 1741 году у него впервые появилось выражение mv²/2^[8].

Томас Юнг в лекциях, опубликованных в 1807 году^[9], предложил вместо термина «живая сила» использовать слово «энергия», хотя первое время после Юнга многие учёные продолжали пользоваться термином "живая сила".

В 1829 году Гаспар-Гюстав Кориолис опубликовал статью Du Calcul de l’Effet des Machines, в которой излагалась математика того, что по сути является связью между работой и кинетической энергией. Исходя из той связи, что существует между механической работой и величиной ${\displaystyle {\frac {1}{2}}mv^{2}}$, Кориолис предложил называть живой силой именно эту величину^[10]. Комментируя такой подход, Кориолис писал^[11]: «Если ранее наименование живая сила давалось произведению массы на квадрат скорости, то это было потому, что не уделялось внимания работе»^[12].

Создание и введение в оборот самого термина «кинетическая энергия» приписывают Уильяму Томсону (лорду Кельвину) c 1849—1851 гг.^[13][14]. Ренкин, который ввёл термин «потенциальная энергия» в 1853 году^[15], позже цитировал У. Томсона и П. Тэйта с заменой слова «кинетическая» на «фактическая»^[16].

По определению, кинетической энергией материальной точки массой ${\displaystyle m}$ называется величина

${\displaystyle T={{mv^{2}} \over 2}}$,

при этом предполагается, что скорость точки ${\displaystyle v}$ всегда значительно меньше скорости света. С использованием понятия импульса (${\displaystyle {\vec {p}}=m{\vec {v}}}$) данное выражение примет вид ${\displaystyle \ T=p^{2}/2m}$.

Если ${\displaystyle {\vec {F}}}$ — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как ${\displaystyle {\vec {F}}=m{\vec {a}}}$. Скалярно умножив его на перемещение материальной точки ${\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t}$ и учитывая, что ${\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}$, причём ${\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}$, получим ${\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}$.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина ${\displaystyle \ T}$ остаётся постоянной, то есть кинетическая энергия является интегралом движения.

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

${\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}$

Здесь ${\displaystyle \ M}$ — масса тела, ${\displaystyle \ v}$ — скорость центра масс, ${\displaystyle {\vec {\omega }}}$ и ${\displaystyle I}$ — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[17].

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ${\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}$. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью ${\displaystyle {\vec {v}}}$, то есть плотность кинетической энергии ${\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V}$ (Дж/м³), запишется:

${\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}$

где по повторяющемуся индексу ${\displaystyle {\alpha }=x,y,z}$, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[18]. Если, в согласии с методом Рейнольдса, представить ${\displaystyle \ \rho ={\overline {\rho }}+\rho '}$, ${\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v'_{\alpha }}$, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

${\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}$

где ${\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2}$ — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, ${\displaystyle E_{t}={\overline {\rho }}\,{\overline {v'_{\alpha }\,v'_{\alpha }}}/2+{\overline {\rho 'v'_{\alpha }v'_{\alpha }}}/2}$ — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[18], часто называемой просто «энергией турбулентности»), а ${\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}}$ — плотность кинетической энергии, связанная с турбулентным потоком вещества (${\displaystyle S_{\alpha }={\overline {\rho 'v'_{\alpha }}}}$ — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения ${\displaystyle E_{s}}$ зависит от выбора системы координат, в то время как кинетическая энергия турбулентности ${\displaystyle E_{t}}$ от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (${\displaystyle {\hat {p}}=-j\hbar \nabla }$, ${\displaystyle \ j}$ — мнимая единица):

${\displaystyle {\hat {T}}={\frac {{\hat {p}}^{2}}{2m}}=-{\frac {\hbar ^{2}}{2m}}\Delta }$

где ${\displaystyle \hbar }$ — редуцированная постоянная Планка, ${\displaystyle \nabla }$ — оператор набла, ${\displaystyle \Delta }$ — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[19].

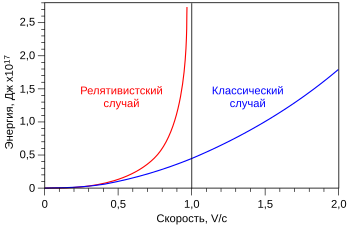
Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как:

${\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}$

где ${\displaystyle \ m}$ — масса материальной точки,

${\displaystyle \ v}$ — скорость движения в выбранной инерциальной системе отсчёта,

${\displaystyle \ c}$ — скорость света в вакууме (${\displaystyle mc^{2}}$ — энергия покоя).

Кинетическая энергия в этой формуле может быть разложена в ряд Маклорена по степеням ${\displaystyle v/c}$:

${\displaystyle T=mc^{2}\left({\frac {1}{2}}(v/c)^{2}+{\frac {3}{8}}(v/c)^{4}+\cdots \right).}$

При скоростях много меньших скорости света (${\displaystyle v\ll c}$) пренебрегаем членами разложения с высшими степенями и выражение для ${\displaystyle \ T}$ переходит в классическую формулу ${\displaystyle \ T\approx 1/2\cdot mv^{2}}$.

Как и в классическом случае, имеет место соотношение ${\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}$, получаемое посредством умножения на ${\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t}$ выражения второго закона Ньютона (в виде ${\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}$).

Релятивистское соотношение между кинетической энергией и импульсом p записывается в виде

${\displaystyle T={\sqrt {p^{2}c^{2}+m^{2}c^{4}}}-mc^{2}=mc^{2}\left({\sqrt {{\frac {p^{2}}{m^{2}c^{2}}}+1}}-1\right).}$

Разложив это выражение по степеням ${\displaystyle p^{2}/(m^{2}c^{2}),}$ получаем

${\displaystyle T=mc^{2}\left({\frac {p^{2}}{2m^{2}c^{2}}}-{\frac {p^{4}}{8m^{4}c^{4}}}+{\frac {3p^{6}}{48m^{6}c^{6}}}-\cdots \right)={\frac {p^{2}}{2m}}-{\frac {p^{4}}{8m^{3}c^{2}}}+{\frac {3p^{6}}{48m^{5}c^{4}}}-\cdots ,}$

первый член которого равен нерелятивистскому выражению кинетической энергии через импульс, а последующие члены — релятивистские поправки к этому выражению, которые малы при ${\displaystyle p\ll mc.}$

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки и направления её скорости, а зависит лишь от модуля скорости или от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[20][21].

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]:

${\displaystyle \ A_{12}=T_{2}-T_{1}.}$

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения ${\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}$ между состояниями 1 и 2).

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

• Теорема о кинетической энергии системы
• Потенциальная энергия
• Закон сохранения энергии
• Хаос
• Энтальпия
• Негэнтропия
• Термодинамика
• Парадокс кинетической энергии

• Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.
• Фриш С. Э. Курс общей физики. В 3-х тт. Т.1. Физические основы механики. Молекулярная физика. Колебания и волны. 13-е изд. — СПб.: Лань, 2010. — 480 с. — ISBN 978-5-8114-0663-0.
• Сивухин Д. В. Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.