Клин (геометрия)
| Клин | |
|---|---|
 | |
| Грани | от 4 до 5 |
| Рёбер | от 6 до 9 |
| Вершин | от 4 до 6 |
| Двойственный многогранник | Треугольная бипирамида |
| Свойства | выпуклый |
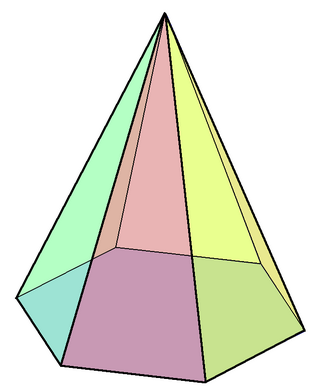
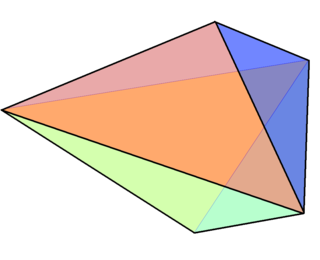
Клин — выпуклый многогранник, образованный на трёх параллельных некомпланарных прямых (образующих), где вершины данного многогранника лежат не более чем по двое на каждой из трёх образующих и не менее чем по одной на каждой из образующих, причём хотя бы на одной из образующих должно обязательно находиться две вершины.
Клин является подклассом призматоидов, если рассматривать верхнее ребро как вырожденную грань (у призматоидов две грани параллельны).
Клин можно также понимать как двуугольный купол.
Сравнение с другими многогранниками:
- Если одна грань параллелепипеда вырождается в отрезок, получится клин.
- Прямоугольная пирамида является клином, в котором одно из рёбер вырождается в точку.
- Треугольная призма, чердак, тетраэдр - клинья.
- Четырёхугольная пирамида с основанием в виде трапеции или параллелограмма - клин.
Объём
Объём клина с прямоугольным основанием вычисляется по формуле
где стороны a, b, c являются длинами отрезков между вершинами, лежащими на одно образующей, а S это площадь ортогонального сечения клина.
Примеры
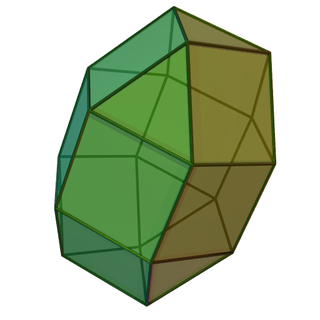
Клинья можно получить разрезанием других многогранников. Например, додекаэдр можно разбить на центральный куб и 6 клиньев, накрывающих грани куба. Ориентации клиньев выбираются таким образом, что треугольные и трапециевидные грани соединяются и образуют правильные пятиугольники.
Треугольная призма является специальным случаем клина с двумя параллельными треугольными гранями.
Два тупых клина можно получить, разрезав пополам правильный тетраэдр плоскостью, параллельной двум противоположным сторонам.
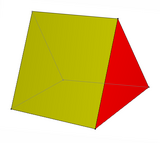 Треугольная призма (Параллельный треугольный клин) | 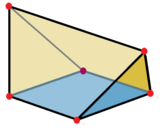 Тупоугольный клин как усечённый наполовину правильный тетраэдр |  Клин, построенный из 8 треугольных граней и 2 квадратов. Его можно рассматривать как тетраэдр, наращенный двумя квадратными пирамидами. | 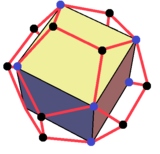 Додекаэдр можно разложить на центральный куб и 6 клиньев на его 6 квадратных гранях. |
Литература
- Harris, J. W., Stocker, H. §4.5.2 // Handbook of Mathematics and Computational Science. — New York: Springer, 1998. — С. 102. — ISBN 978-0-387-94746-4.