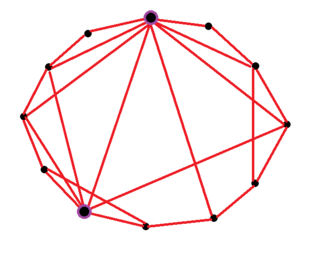
Комплексные сети

Сложные се́ти или комплексные сети (англ. complex networks) — это существующие в природе сети (графы), обладающие нетривиальными топологическими свойствами.

Большинство объектов природы и общества имеют бинарные связи, которые можно представить в виде сети, где каждый объект — это точка, а его связь с другим объектом — это линия или дуга.

Так, отношения между государствами, людьми в группе (см. социальная сеть (социология)), отношения между фирмами, компьютерные сети, Веб, отношения между генами в ДНК — всё это примеры сетей^[1][2][3].

Топологические свойства этих сетей (см. топология), рассматриваемые отвлечённо от их физической природы, но существенно определяющие функционирование сетей, и составляют предмет исследования комплексных сетей.

Сложные сети — это относительно новая, бурно развивающаяся междисциплинарная область знаний. Сейчас закладываются её основные понятия и получены только первые результаты. Работающие в этой области исследователи пришли из математики, компьютерных наук, физики, биологии, социологии, экономики. Соответственно, результаты исследований имеют как теоретическое значение, так и практические приложения в этих науках. В работе ^[4] отмечается, что термин «сложная сеть», как правило, употребляется для обозначения реальной исследуемой системы, в то время как термин «сложный граф» обычно используют для обозначения математической модели такой системы.

Наибольшие разночтения вызывает термин «сложный». Как правило, термин «сложный» трактуется в двух вариантах:

I. Плоские сети (графы) очень большой размерности. Такие сети могут включать миллионы и более вершин. Ребра, соединяющие вершины, могут быть ненаправленными или направленными. Иногда используется модель мультиграфа, в этом случае две вершины могут соединяются не одним, а несколькими ребрами. Именно такую модель в литературе чаще всего называют «сложной сетью». Исследования данной модели проводятся в основном специалистами в области математики. Исследователи рассматривают такие параметры как распределение количества связей между вершинами, выделение сильно связанных подграфов. Часто для связей вводится количественная метрика, которая обычно трактуется как расстояние между вершинами. Активно исследуются динамические модели, в которых к существующей сложной сети случайным образом добавляются вершины и ребра. Такие модели представляют интерес при изучении социальных сетей, глобальных компьютерных сетей, различных социологических и биологических моделей. Но они не очень хорошо помогают при описании сложных моделей данных.

II. Сложные сети (графы), в которых используется сложное (комплексное) описание вершин, ребер и/или их расположения. Часто в таких моделях отказываются от плоского расположения вершин и ребер. Именно подобные модели могут быть наиболее полезны при описании сложных моделей данных. На сегодняшний день известны четыре подобных модели: гиперсеть, гиперграфф, метаграф и многоуровневая сеть (которая является упрощенным вариантом гиперсети).

Каждый узел сети (node) может быть связан с другими узлами определённым числом связей (links). Связи между узлами могут иметь направление. В этом случае сеть называется ориентированной (directed network). Если связь симметрична для обеих связанных ею узлов, то образованная такими связями сеть называется неориентированной сетью (undirected network). Например, Веб — это ориентированная сеть, а интернет — неориентированная сеть. Иногда вопрос об ориентированности сети не столь тривиален. Например, отношения между людьми. Если считать, что связь существует, если две персоны являются близкими друзьями, то сеть будет неориентированной. Если считать, что связь существует, если одна персона считает себя другом другой, то образованная сеть будет ориентированной. Отдельные виды сложных политических сетей развиваются в международных организациях. Этому посвящена статья А. С. Бояшова, в которой рассмотрены следующие типы сетей: дипломатические (формирующиеся между государствами), институциональные (между международными организациями), организационные (между НКО)^[3].

Число связей узла будем называть степенью (degree) узла. Для ориентированных сетей различают исходящую и входящую степени узла (out degree и in degree). Распределение степеней узлов является важной характеристикой сложной сети. Большинство сложных сетей имеют близкое к степенному закону распределение степеней узлов с показателем степени между 2 и 3.

Минимальное число связей, которое необходимо преодолеть, чтобы попасть из узла в узел, называется расстоянием между узлами. Усреднённое расстояние между всеми парами узлов сети, для которых существует путь перехода из одного в другой, называется средним расстоянием между узлами ${\displaystyle d}$. Для большинства комплексных сетей ${\displaystyle d\sim \log(N)}$ , где ${\displaystyle N}$ — количество узлов в сети.

Будем называть два узла соседями, если существует связь между ними. Для комплексных сетей характерно, что два узла, соседних к какому-либо узлу, часто также являются соседями между собой. Чтобы охарактеризовать это явление и был предложен кластерный коэффициент ${\displaystyle C_{i}}$ узла ${\displaystyle i}$. Предположим, что узел имеет степень ${\displaystyle k_{i}}$ , это значит, что у него ${\displaystyle k_{i}}$ соседей и между ними может быть максимум ${\displaystyle k_{i}(k_{i}-1)/2}$ связей. Тогда

${\displaystyle C_{i}={\frac {2n_{i}}{k_{i}(k_{i}-1)}},}$

где ${\displaystyle n_{i}}$ — число связей между соседями узла ${\displaystyle i}$. Очевидно, что всегда ${\displaystyle 0\leqslant C_{i}\leqslant 1}$. Усреднённый кластерный коэффициент узлов называется кластерным коэффициентом сети. Для большинства сложных сетей он существенно больше, чем кластерный коэффициент случайного графа таких же размеров.

В сети возможна ситуация, когда узлы, имеющие большую степень («звёзды»), преимущественно связаны с узлами, имеющими большую степень. Иными словами «звёзды» «предпочитают» быть связанными со «звёздами». Такие сети называют ассортативными. Возможна также обратная ситуация: «звёзды» связаны с другими «звёздами» через цепочки узлов, имеющих малое число соседей. Такие сети называют дисассортативными. Чтобы охарактеризовать это свойство, пользуются коэффициентом ассортативности ${\displaystyle r}$ — так называется коэффициент корреляции Пирсона между степенью соседних узлов. По определению, ${\displaystyle -1\leqslant r\leqslant 1}$. Для ассортативных сетей ${\displaystyle r>0}$, для дисассортативных сетей ${\displaystyle r<0}$. Сети, связанные с общественными явлениями, являются ассортативными. Сети, связанные с биологическими явлениями, чаще дисассортативны. Существуют сети, не имеющие выраженной ассортативности с ${\displaystyle r}$ близким к нулю.

• Модель Барабаси-Альберта