Конфигурация Кремоны — Ричмонда

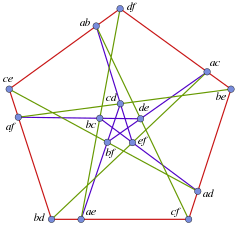
Конфигурация Кремоны — Ричмонда — конфигурация из 15 прямых и 15 точек, по три точки, лежащих на каждой прямой, и через каждую точку проходят 3 прямых, при этом конфигурация не содержит треугольников. Конфигурацию изучали Кремона (Cremona 1877) и Ричмонд^[англ.] (Richmond 1900). Конфигурация является обобщённым четырёхугольником с параметрами (2,2). Граф Леви конфигурации — это граф Татта — Коксетера.^[1]

Симметрия

Точки конфигурации Кремоны — Ричмонда можно отождествить с $15={\binom {6}{2}}$ неупорядоченными парами элементов множества из шести элементов, прямые же конфигурации можно отождествить с 15 способами разложения этих шести элементов на три пары, при этом точка инцидентна прямой (лежит на прямой) в том и только в том случае, когда соответствующая пара элементов содержится в разложении, соответствующем прямой. В этой схеме пары элементов называются двойками (duads), а разложения на три пары называются наборами (synthemes). Таким образом, симметрическая группа шести элементов действует транзитивно на флаги конфигурации, где флаг — это пара — прямая и точка на ней. Эта группа является группой автоморфизмов конфигурации.^[1]

Конфигурация Кремоны — Ричмонда является самодвойственной — можно обменять местами точки и прямые, сохраняя при этом все свойства инцидентности конфигурации. Эта двойственность придаёт графу Татта — Коксетера дополнительные симметрии, не принадлежащие симметриям конфигурации Кремоны — Ричмонда, которые меняют местами обе доли двудольного графа. Эти симметрии соответствуют внешним автоморфизмам^[англ.] симметрической группы шести элементов.

Реализация

Любые шесть точек в общем положении в четырёхмерном пространстве дают 15 точек, которые определяются пересечением прямых, проходящих через две точки, с гиперплоскостями, которые определяют оставшиеся четыре точки. Таким образом, двойки соответствуют один к одному этим полученным 15 точкам. Любые три двойки, которые вместе образуют набор, задают прямую, являющуюся пересечением трёх гиперплоскостей, содержащих две из трёх троек из набора, и эта прямая содержит все точки, соответствующие трём двойкам набора. Таким образом, двойки и наборы абстрактной конфигурации один к одному соответствуют, в смысле принадлежности точек прямым, этим 15 точкам и 15 прямым, полученным из начальных шести точек. То же самое построение можно спроектировать в евклидово пространство (3- мерное) или евклидову плоскость.^[1]

Конфигурация Кремоны — Ричмонда имеет также семейство реализаций на плоскости, зависящее от одного параметра, которое имеет циклическую симметрию пятого порядка.^[2]

История

Шлефли (Schläfli 1858)(Schläfli 1863) нашёл кубические поверхности, содержащие 15 вещественных прямых (дополнительных к двойной шестёрке Шлефли во множестве 27 прямых кубики) и 15 касательных плоскостей, по три прямых на каждой плоскости и по три плоскости, проходящих через каждую прямую. Пересечение этих прямых и плоскостей с ещё одной плоскостью даёт 15₃15₃ конфигурацию. Эта модель инциденций прямых и плоскостей Шлефли была позднее опубликована Кремоной (Cremona 1868). Наблюдение, что полученная конфигурация не содержит треугольников, было сделано Мартинетти (Martinetti 1886). Та же самая конфигурация появилась в работе Ричмонда (Richmond 1900). Висконти (Visconti 1916) обнаружил, что конфигурацию можно представить в виде самовписанного многоугольника. Бейкер^[англ.] использовал четырёхмерную реализацию конфигурации в качестве рисунка на обложке его двухтомной работы 1922—1925 Principles of Geometry (Основы геометрии). Захарис (Zacharias 1951) переоткрыл ту же самую конфигурацию и обнаружил её реализацию с циклической симметрией пятого порядка.^[3]

Название конфигурации произошло от работ Кремоны (Cremona 1868)(Cremona 1877) и Ричмонда (Richmond 1900). Возможно, вследствие некоторых ошибок в работах Мартинетти его вклад остался незамеченным.^[3]

Примечания

↑ ¹ ² ³ Coxeter, 1950; Coxeter, 1958. Термины двойки (duads) и наборы (synthemes) взяты из статьи Сильвестера (Sylvester 1844), но Сильвестер использовал эти системы пар и разложений в контексте более общих исследований комплектов и разложений множеств, не уделяя особого внимания множеству из шести элементов и не связывал эти множества с геометрией.
↑ Zacharias, 1951; Boben, Pisanski, 2003; Boben, Grünbaum, Pisanski, Žitnik, 2006.
↑ ¹ ² История конфигурации Кремоны — Ричмонда и большинство ссылок взяты из статьи Boben, Grünbaum, Pisanski, Žitnik, 2006. Ссылка на Бейкера взята из статьи Коксетера (Coxeter 1950).

Литература

M. Boben, T. Pisanski. Polycyclic configurations // European Journal of Combinatorics. — 2003. — Т. 24, вып. 4. — С. 431–457. — doi:10.1016/S0195-6698(03)00031-3.
Marko Boben, Branko Grünbaum, Tomaž Pisanski, Arjana Žitnik. Small triangle-free configurations of points and lines // Discrete and Computational Geometry. — 2006. — Т. 35, вып. 3. — С. 405–427. — doi:10.1007/s00454-005-1224-9..
H. S. M. Coxeter. Self-dual configurations and regular graphs // Bulletin of the American Mathematical Society. — 1950. — Т. 56. — С. 413–455. — doi:10.1090/S0002-9904-1950-09407-5..
H. S. M. Coxeter. Twelve points in PG(5,3) with 95040 self-transformations // Proceedings of the Royal Society A. — 1958. — Т. 247, вып. 1250. — С. 279–293. — doi:10.1098/rspa.1958.0184. — JSTOR 100667..
L. Cremona. Mémoire de géométrie pure sur les surfaces du troisieme ordre // J. Reine Angew. Math.. — 1868. — Т. 68. — С. 1–133.. Как цитировано в Boben, Grünbaum, Pisanski, Žitnik, 2006.
L. Cremona. {{{заглавие}}}. — 1877. — Т. 1.
Branko Grünbaum. Configurations of points and lines. — Providence, R.I.: American Mathematical Society, 2009. — Т. 103. — (Graduate Studies in Mathematics). — ISBN 978-0-8218-4308-6.
Sopra alcune conﬁgurazioni piane // Annali di matematica pura ed applicata. — 1886. — Т. 14, вып. 1. — С. 161–192. — doi:10.1007/BF02420733..
H. W. Richmond. On the figure of six points in space of four dimensions. // Quart. J.. — 1900. — Т. 31. — С. 125–160.
L. Schläfli. An attempt to determine the twenty-seven lines upon a surface of the third order, and to divide such surfaces into species in reference to the reality of the lines upon the surface // Quart. J. Pure Appl. Math.. — 1858. — Т. 2. — С. 55–65, 110–120..
L. Schläfli. On the distribution of surfaces of the third order into species, in reference to the absence or presence of singular points, and the reality of their lines // Philosophical Transactions of the Royal Society. — 1863. — Т. 153. — С. 193–241. — doi:10.1098/rstl.1863.0010..
Elementary researches in the analysis of combinatorial aggregation // The Philos. Mag.. — 1844. — Т. 24. — С. 285–295..
E. Visconti. Sulle conﬁgurazioni piane atrigone // Giornale di Matematiche di Battaglini. — 1916. — Т. 54. — С. 27–41.. Как цитировано в Boben, Grünbaum, Pisanski, Žitnik, 2006.
Max Zacharias. Streifzüge im Reich der Konfigurationen: Eine Reyesche Konfiguration (15₃), Stern- und Kettenkonfigurationen // Mathematische Nachrichten. — 1951. — Т. 5. — С. 329–345. — doi:10.1002/mana.19510050602..