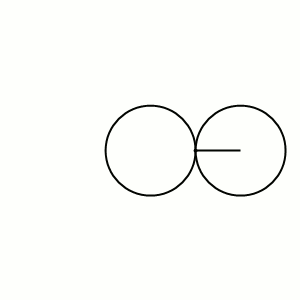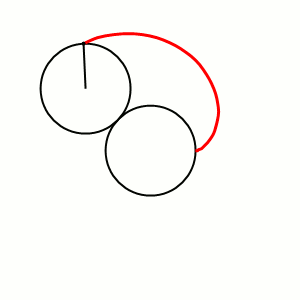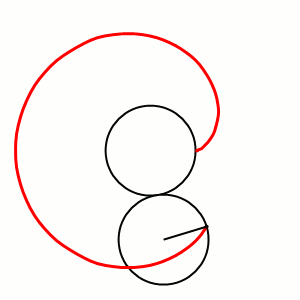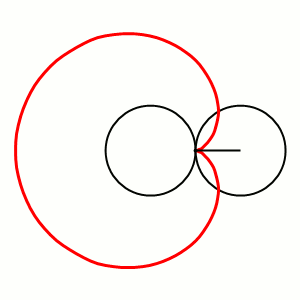Конхоидное преобразование

Конхо́идное преобразова́ние (англ. conchoidal transform, от др.-греч. κονχοειδής — похожий на раковину) — точечное преобразование плоскости, переводящее точку в конхоиду — точку, радиус-вектор которой увеличен или уменьшен на постоянную величину относительно радиус-вектора исходной точки^[1].

Если полюс бесконечно удалён, то конхоидное преобразование вырождается в параллельный перенос с фиксированным направлением.

При нулевом радиус-векторе конхоидное преобразование не определено.

Если координаты исходной точки в полярной системе координат ${\displaystyle (r,\,\varphi ),\,}$ то координаты преобразованной ${\displaystyle (r+l,\,\varphi ),\,}$ то есть уравнение конхоидного преобразования имеет следующий вид (см. рисунок справа вверху в начале статьи)^[1][2]:

${\displaystyle r'=r+l,\,}$ ${\displaystyle \varphi '=\varphi .}$

Начало радиус-вектора называется полюсом конхоиды (в данном случае это начало координат ${\displaystyle (0,\,0)\,}$), а постоянная величина приращения радим-вектора ${\displaystyle l\,}$ — модулем конхоиды^[2]. Направление радиус-вектора называется направлением конхоиды.

Конхоидные преобразования ${\displaystyle r'=r+l}$ с фиксированным полюсом и направлением образуют:

• точки вещественной прямой ${\displaystyle \mathbb {R} }$ с координатами ${\displaystyle l}$;
• абелеву группу, изоморфную группе параллельных переносов ${\displaystyle \mathbb {R} }$, то есть группе сложения вещественных чисел, поскольку выполняются два свойства этого преобразования^[3]:

• композиция двух конхоидных преобразований есть конхоидное преобразование:

${\displaystyle r''\circ r'=(r+l'')\circ (r+l')=(r+l')+l''=}$

${\displaystyle =r+(l'+l'')=r+l''';}$

• преобразование, обратное конхоидному преобразованию ${\displaystyle r=r+l}$, есть конхоидное преобразование ${\displaystyle r^{-1}=r-l}$:

${\displaystyle (r-l)\circ (r+l)=(r+l)-l=r.}$

Конхоидные преобразования ${\displaystyle r'=r+l}$ только с фиксированным полюсом образуют точки проективно-вещественной плоскости ${\displaystyle \mathbb {P} \times \mathbb {R} }$ с координатами ${\displaystyle ((r\cos \varphi ,\,r\sin \varphi );\,l)}$ и не образуют группу, поскольку конхоидные преобразования с фиксированными полюсом и разными направлениями не образуют композиции.

На комплексной плоскости уравнение конхоидного преобразования с полюсом в начале координат имеет следующий вид (см. рисунок справа вверху)^[1]:

${\displaystyle z'=z+l{\sqrt {\frac {z}{\bar {z}}}}=z+l{\frac {z}{|z|}}=z+le^{i\varphi },}$

где ${\displaystyle e^{i\varphi }}$ — единичный вектор, определяющий направление конхоидного преобразования от полюса ${\displaystyle (0,\,0)\,}$ к произвольной точке плоскости ${\displaystyle z=x+iy;\,}$ ${\displaystyle \cos \varphi ={\frac {x}{|z|}};\,}$ ${\displaystyle \sin \varphi ={\frac {y}{|z|}}.}$

Обычное уравнение конхоидного преобразования с полюсом в начале координат произвольной точки декартовой плоскости имеет следующий вид:

${\displaystyle a'=a+l{\frac {a}{|a|}}=a+le,}$

где ${\displaystyle e\,}$ — единичный вектор, определяющий направление конхоидного преобразования от полюса к произвольной точке пространства ${\displaystyle a}$ (см. рисунок справа вверху).

На декартовой плоскости конхоидное преобразование с полюсом в начале координат имеет следующий параметрический вид как декартовых координат конхоиды ${\displaystyle r'=r+l}$ (см. рисунок справа вверху)^[4][5]:

${\displaystyle x=x(t)\left(1+{\frac {l}{\sqrt {x^{2}(t)+y^{2}(t)}}}\right),}$

${\displaystyle y=y(t)\left(1+{\frac {l}{\sqrt {x^{2}(t)+y^{2}(t)}}}\right),}$

а с произвольным полюсом ${\displaystyle (x_{0},\,y_{0})}$ — более сложный параметрический вид^[5]:

${\displaystyle x=x(t)+\left({\frac {l(x(t)-x_{0})}{\sqrt {(x(t)-x_{0})^{2}+(y(t)-y_{0})^{2}}}}\right),}$

${\displaystyle y=y(t)+\left({\frac {l(y(t)-y_{0})}{\sqrt {(x(t)-x_{0})^{2}+(y(t)-y_{0})^{2}}}}\right),}$

Конхоидное преобразование используется для образования новых плоских кривых — конхоид из исходных — директрис^[6], или базисов^[7]. В этом случае его уравнение могут записать в виде

${\displaystyle r(\varphi )=f(\varphi )\pm l,\,}$ ${\displaystyle l>0,}$

где ${\displaystyle r(\varphi )=f(\varphi )}$ — уравнение директрисы. и говорить о ${\displaystyle 2m}$ ветвях конхоиды, которые соответствуют прибавлению и вычитанию положительной константы ${\displaystyle l}$ к координатам ${\displaystyle f(\varphi ),\,}$ соответствующим ${\displaystyle m}$ точкам — максимальному количеству точек пересечения директрисы с произвольной прямой ${\displaystyle \varphi =\varphi _{0}}$. Обычно рассматривают случаи с ${\displaystyle m=1}$^{[1][2][8][4][5]}.

Например, конхоида Никомеда как конхоида прямой и улитка Паскаля как конхоида окружности с полюсом на окружности относятся к случаю ${\displaystyle m=1,\,}$ а конхоида конхоиды — вторая конхоида — и конхоида окружности, когда полюс не лежит на окружности — к случаю ${\displaystyle m=2.}$

При ${\displaystyle l=0}$ конхоида совпадает со своей директрисой, а при ${\displaystyle l\to \infty }$ — с бесконечно удалёнными точками на окружности бесконечного радиуса.

При ${\displaystyle f(\varphi _{0})=0}$ угол ${\displaystyle \varphi _{0}}$ выбирается по непрерывности конхоиды.

Конхоиды ${\displaystyle r=f+l}$ с фиксированным полюсом, аналогично точечным конхоидным преобразованиям, образуют (если ветвей несколько, то берётся нужная):

• точки вещественной прямой ${\displaystyle \mathbb {R} }$ с координатами ${\displaystyle l}$;
• коммутативную группу, изоморфную группе параллельных переносов ${\displaystyle \mathbb {R} }$, то есть группе сложения вещественных чисел, поскольку выполняются два свойства этого преобразования^[3]:

Когда обе ветви конхоиды совпадают, то есть совпадают кривые

${\displaystyle r(\varphi )=f(\varphi )+l,\,}$ ${\displaystyle r(\varphi )=f(\varphi )-l,\,}$ ${\displaystyle l>0,}$

директриса ${\displaystyle f(\varphi )}$ называется минимальной конхоидой, поскольку любая конхоида с этой первоначальной директрисой не может быть «меньше» минимальной конхоиды: для любой первой конхоиды минимальной директрисы

${\displaystyle r(\varphi )=f(\varphi )\pm l,\,}$ ${\displaystyle l>0}$

две из четырёх ветвей второй конхоиды (с первой конхоидой как директрисой)

${\displaystyle r(\varphi )=(f(\varphi )\pm l)\mp 2l,\,}$ ${\displaystyle l>0}$

совпадают друг с другом и с исходной первой конхоидой.

Например, минимальная конхоида — базовая окружность улитки Паскаля.

В общем случае полюс конхоидного преобразования может быть произвольным, то есть уравнение конхоидного преобразования на комплексной плоскости имеет следующий вид (см. рисунок справа):

${\displaystyle z'=z+l{\sqrt {\frac {z-z_{0}}{\overline {z-z_{0}}}}}=}$

${\displaystyle =z+l{\frac {z-z_{0}}{|z-z_{0}|}}=}$

${\displaystyle =z+le^{i\varphi },}$

где ${\displaystyle z_{0}=x_{0}+iy_{0}\,}$ — полюс; ${\displaystyle l\,}$ — модуль; ${\displaystyle e^{i\varphi }\,}$ — единичный вектор, определяющий направление конхоидного преобразования от полюса к произвольной точке плоскости ${\displaystyle z=x+iy;\,}$ ${\displaystyle \cos \varphi ={\frac {x-x_{0}}{|z-z_{0}|}};\,}$ ${\displaystyle \sin \varphi ={\frac {y-y_{0}}{|z-z_{0}|}}.}$

Если полюс бесконечно удалён, то конхоидное преобразование вырождается в параллельный перенос.

При нулевом радиус-векторе конхоидное преобразование не определено.

Два конхоидных преобразования ${\displaystyle z'=z+le^{i\varphi }\,}$ и ${\displaystyle z''=z'+l'e^{i\varphi '},\,}$ действующие на одной прямой, эквивалентны на прямой, если результаты их действия совпадают, то есть если равны их модули и направления (полюса могут различаться):

${\displaystyle l=l',\,}$ ${\displaystyle e^{i\varphi }=e^{i\varphi '},\,}$ ${\displaystyle z,\,z',\,z''}$ коллинеарны.

Конхоидные преобразования ${\displaystyle z'=z+le^{i\varphi }}$, действующие на одной прямой, с точностью до эквивалентных преобразований образуют:

• точки вещественной прямой ${\displaystyle \mathbb {R} }$ с координатами ${\displaystyle l}$;
• абелеву группу, изоморфную группе параллельных переносов ${\displaystyle \mathbb {R} }$, то есть группе сложения вещественных чисел.

Два произвольных конхоидных преобразования ${\displaystyle z'=z+le^{i\varphi }\,}$ и ${\displaystyle z''=z'+l'e^{i\varphi '}\,}$ эквивалентны, если результаты их действия совпадают, то есть если равны их модули и направления (полюса могут различаться):

${\displaystyle l=l',\,}$ ${\displaystyle e^{i\varphi }=e^{i\varphi '}.}$

Конхоидные преобразования ${\displaystyle z'=z+le^{i\varphi }}$ одинакового направления с точностью до эквивалентных преобразований образуют точки вещественной плоскости ${\displaystyle \mathbb {R} ^{2}}$ с координатами ${\displaystyle (x+y,\,l)}$ и не образуют группу, поскольку конхоидные преобразования одного направления, не лежащие на одной прямой, не образуют композиции.

Конхоидное преобразование имеет обратное преобразование ${\displaystyle z^{-1}=z-le^{i\varphi }:}$

${\displaystyle z-le^{i\varphi }\circ z+le^{i\varphi }=z+le^{i\varphi }-le^{i\varphi }=z,\,}$

а также композиция двух конхоидных преобразований есть снова конхоидное преобразование, так как сумма комплексных чисел есть снова комплексное число:

${\displaystyle z''\circ z'=z'+l'e^{i\varphi '}\circ z+le^{i\varphi }=z+le^{i\varphi }+l'e^{i\varphi '}=}$

${\displaystyle =z+l''e^{i\varphi ''}=z+l''{\frac {z-z''_{0}}{|z-z''_{0}|}},}$

другими словами, конхоидные преобразования ${\displaystyle z'=z+le^{i\varphi }}$ с точностью до эквивалентных преобразований образуют коммутативную группу, изоморфную группе параллельных переносов ${\displaystyle \mathbb {R} ^{2}}$, то есть группе сложения радиус-векторов плоскости, поскольку выполняются эти два групповые свойства^[3].

Вычисление полюса и модуля композиции двух конхоидных преобразований

Пусть заданы два конхоидных преобразования своими полюсами соответственно ${\displaystyle z_{0}=x_{0}+iy_{0}\,}$ и ${\displaystyle z_{0}'=x_{0}'+iy_{0}'\,}$ и модулями соответственно ${\displaystyle l\,}$ и ${\displaystyle l',\,}$ а также задана исходная произвольная точка плоскости ${\displaystyle z=x+iy\,}$ (см. рисунок справа). Тогда первая конхоида ${\displaystyle z'}$ исходной точки ${\displaystyle z}$ равна

${\displaystyle z'=z+le^{i\varphi },\,}$ ${\displaystyle \cos \varphi ={\frac {x-x_{0}}{|z-z_{0}|}};\,}$ ${\displaystyle \sin \varphi ={\frac {y-y_{0}}{|z-z_{0}|}},\,}$

а конхоида ${\displaystyle z''}$ первой конхоиды ${\displaystyle z'}$ (вторая конхоида исходной точки) равна

${\displaystyle z''=z'+l'e^{i\varphi '},\,}$ ${\displaystyle \cos \varphi '={\frac {x'-x_{0}'}{|z'-z_{0}'|}};\,}$ ${\displaystyle \sin \varphi '={\frac {y'-y_{0}'}{|z'-z_{0}'|}}.}$

Из композиции двух конхоидных преобразования

${\displaystyle z'\circ z=z+le^{i\varphi }+l'e^{i\varphi '}=z+l''e^{i\varphi ''},\,}$

${\displaystyle \cos \varphi ''={\frac {x-x_{0}''}{|z-z_{0}''|}};\,}$ ${\displaystyle \sin \varphi ''={\frac {y-y_{0}''}{|z-z_{0}''|}},\,}$

получаем два уравнения

${\displaystyle l''\cos \varphi ''=l\cos \varphi +l'\cos \varphi ',\,}$

${\displaystyle l''\sin \varphi ''=l\sin \varphi +l'\sin \varphi ',\,}$

из которых вычисляем модуль ${\displaystyle l''}$ композиции (см. рисунок справа вверху)

${\displaystyle l''^{2}=(l\cos \varphi +l'\cos \varphi ')^{2}+(l\sin \varphi +l'\sin \varphi ')^{2}=}$

${\displaystyle =l^{2}+l'^{2}+2ll'(\cos \varphi \cos \varphi '+\sin \varphi \sin \varphi ')=}$

${\displaystyle =l^{2}+l'^{2}+2ll'\cos(\varphi '-\varphi ),}$

где ${\displaystyle \pi -(\varphi '-\varphi )}$ — угол при вершине ${\displaystyle z'}$ треугольника ${\displaystyle zz'z''}$ (получили теорему косинусов).

Для вычисления полюса ${\displaystyle z_{0}''=x_{0}''+iy_{0}''}$ одного из преобразований, эквивалентного композиции, предположим, что

${\displaystyle z''-z=z-z_{0}'',\,}$

откуда (см. рисунок справа вверху)

${\displaystyle z_{0}''=2z-z''.}$

Уравнение общего конхоидного преобразования произвольной точки ${\displaystyle n}$-мерного декартового пространства имеет следующий вид:

${\displaystyle a'=a+l{\frac {a-a_{0}}{|a-a_{0}|}}=a+le,}$

где ${\displaystyle a_{0}=(a_{01},\,a_{02},\,\dots ,\,a_{0n})\,}$ — полюс; ${\displaystyle l\,}$ — модуль; ${\displaystyle e=(e_{1},\,e_{2},\,\dots ,\,e_{n})\,}$ — единичный вектор, определяющий направление конхоидного преобразования от полюса к произвольной точке пространства ${\displaystyle a=(a_{1},\,a_{2},\,\dots ,\,a_{n}).}$

Если полюс бесконечно удалён, то конхоидное преобразование вырождается в параллельный перенос.

При нулевом радиус-векторе конхоидное преобразование не определено.

Два конхоидных преобразования ${\displaystyle a'=a+le}$ и ${\displaystyle a''=a'+l'e,}$ действующие на одной прямой, эквивалентны на прямой, если результаты их действия совпадают, то есть если равны их модули и направления (полюса могут различаться):

${\displaystyle l=l',\,}$ ${\displaystyle e=e',\,}$ ${\displaystyle a,\,a',\,a''}$ коллинеарны.

Конхоидные преобразования ${\displaystyle a'=a+le}$, действующие на одной прямой, с точностью до эквивалентных преобразований образуют:

• точки вещественной прямой ${\displaystyle \mathbb {R} }$ с координатами ${\displaystyle l}$;
• абелеву группу, изоморфную группе параллельных переносов ${\displaystyle \mathbb {R} }$, то есть группе сложения вещественных чисел.

Два конхоидных преобразования ${\displaystyle a'=a+le\,}$ и ${\displaystyle a''=a'+le'\,}$ эквивалентны, если результаты их действия совпадают, то есть если равны их модули и направления (полюса могут различаться):

${\displaystyle l=l',\,}$ ${\displaystyle e=e'.}$

Конхоидные преобразования ${\displaystyle a'=a+le}$ одинакового направления с точностью до эквивалентных преобразований образуют точки ${\displaystyle n}$-мерного вещественного пространства ${\displaystyle \mathbb {R} ^{n}}$ с координатами

${\displaystyle (a_{1}+a_{2},\,a_{2}+a_{3},\,\dots ,\,a_{n-1}+a_{n},\,l)}$

и не образуют группу, поскольку конхоидные преобразования одного направления, не лежащие на одной прямой, не образуют композиции.

Конхоидное преобразование имеет обратное преобразование ${\displaystyle a^{-1}=a-le:}$

${\displaystyle a-le\circ z+le=a+le-le=a,\,}$

а также композиция двух конхоидных преобразований есть снова конхоидное преобразование, так как сумма радиус-векторов есть снова радиус-вектор:

${\displaystyle a'''=a''\circ a'=a'+l'e'\circ a+le=a+le+l'e'=}$

${\displaystyle =a+l''e''=a+l''{\frac {a-a''_{0}}{|a-a''_{0}|}},}$

другими словами, конхоидное преобразование ${\displaystyle a'=a+le}$ с точностью до эквивалентных преобразований образует коммутативную группу, изоморфную группе параллельных переносов ${\displaystyle \mathbb {R} ^{n}}$, то есть группе сложения радиус-векторов пространства, поскольку выполняются эти два групповые свойства^[3].

Вычисление полюса и модуля композиции двух конхоидных преобразований

Пусть заданы два конхоидных преобразования своими полюсами соответственно ${\displaystyle a_{0}=(a_{01},\,a_{02},\,\dots ,\,a_{0n})\,}$ и ${\displaystyle a_{0}'=(a_{01}',\,a_{02}',\,\dots ,\,a_{0n}')\,}$ и модулями соответственно ${\displaystyle l\,}$ и ${\displaystyle l',\,}$ а также задана исходная произвольная точка плоскости ${\displaystyle a=(a_{1},\,a_{2},\,\dots ,\,a_{n})\,}$ (см. рисунок справа для трёхмерного пространства). Тогда первая конхоида ${\displaystyle a'}$ исходной точки ${\displaystyle a}$ равна

${\displaystyle a'=a+le,\,}$ ${\displaystyle e={\frac {a-a_{0}}{|a-a_{0}|}},}$

а конхоида ${\displaystyle a''}$ первой конхоиды ${\displaystyle a'}$ (вторая конхоида исходной точки) равна

${\displaystyle a''=a'+l'e',\,}$ ${\displaystyle e'={\frac {a'-a_{0}'}{|a'-a_{0}'|}}.}$

Из композиции двух конхоидных преобразования

${\displaystyle a'''=a''\circ a'=a+le+l'e'=a+l''e'',\,}$ ${\displaystyle e''={\frac {a''-a_{0}''}{|a''-a_{0}''|}}}$

получаем ${\displaystyle n}$ уравнений, ${\displaystyle i=1,\,2,\,\dots ,n:}$

${\displaystyle l''e''_{i}=le_{i}+l'e'_{i},}$

из которых вычисляем модуль ${\displaystyle l''}$ композиции (см. рисунок справа вверху для трёхмерного пространства)

${\displaystyle l''^{2}=\sum _{i=1}^{n}(le_{i}+l'e'_{i})^{2}=}$

${\displaystyle =l^{2}+l'^{2}+2ll'\sum _{i=1}^{n}(e_{i}\cdot e'_{i})=}$

${\displaystyle =l^{2}+l'^{2}+2ll'\cos \angle (e,\,e'),}$

${\displaystyle =l^{2}+l'^{2}-2ll'\cos \angle aa'\!a'',}$

где ${\displaystyle \angle aa'\!a''=\pi -\angle (e,\,e')}$ (получили теорему косинусов).

Для вычисления полюса ${\displaystyle a_{0}''=(a_{01}'',\,a_{02}'',\,\dots ,\,a_{0n}'')\,}$ одного из преобразований, эквивалентного композиции, предположим, что

${\displaystyle a''-a=a-a_{0}'',}$

откуда (см. рисунок справа вверху для трёхмерного пространства)

${\displaystyle a_{0}''=2a-a''.}$

На рисунке видно, что Исходная точка и обе её конхоиды лежат в одной плоскости композиции.

• Ефимов Н. В. Высшая геометрия. 7-е изд. М.: ФИЗМАТЛИТ, 2004. 584 с. ISBN 5-9221-0267-2.
• Савелов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство) / Под ред. А. П. Нордена. М.: Физматлит, 1960. 293 с., ил.
• Ferréol Robert. Conchoid // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 6 марта 2023 на Wayback Machine
• jan wassenaar conchoid // mathematical curves Архивная копия от 4 октября 2023 на Wayback Machine
• Weisstein Eric W. Conchoid // Wolfram MathWorld Архивная копия от 25 декабря 2023 на Wayback Machine
• Zwikker C.^[англ.] The Advanced Geometry of Plane Curves and Their Applications^[англ.]The Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.