
О́птика — раздел физики, изучающий поведение и свойства света, в том числе его взаимодействие с веществом и создание инструментов, которые его используют или детектируют. Оптика обычно описывает поведение видимого, ультрафиолетового и инфракрасного излучения. Поскольку свет представляет собой электромагнитную волну, другие формы электромагнитного излучения, такие как рентгеновские лучи, микроволны и радиоволны, обладают аналогичными свойствами.

Свет — электромагнитное излучение, воспринимаемое человеческим глазом. В качестве коротковолновой границы спектрального диапазона, занимаемого светом, принят участок с длинами волн в вакууме 380−400 нм, а в качестве длинноволновой границы — участок 760−780 нм.

Волна́ — изменение некоторой совокупности физических величин, которое способно перемещаться, удаляясь от места их возникновения, или колебаться внутри ограниченных областей пространства.
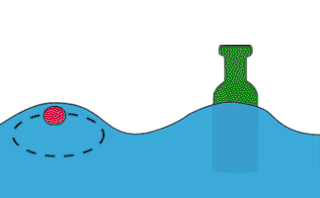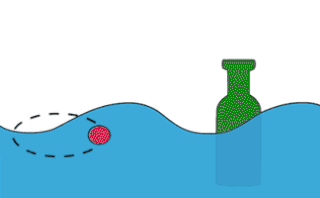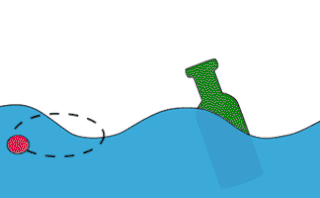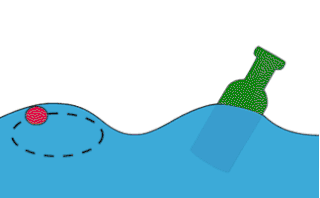
Гравитацио́нные во́лны на воде́ — разновидность волн на поверхности жидкости, при которых сила, возвращающая деформированную поверхность жидкости к состоянию равновесия, есть просто сила тяжести, связанная с перепадом высот гребня и впадины в гравитационном поле.
Зако́н диспе́рсии, или дисперсионное соотношение, в теории волн — функция зависимости частоты волны от волнового вектора:
 .
.

Эффе́кт До́плера — изменение частоты и, соответственно, длины волны излучения, воспринимаемое наблюдателем (приёмником), вследствие движения источника излучения относительно наблюдателя (приёмника). Эффект назван в честь австрийского физика Кристиана Доплера.

Дифра́кция во́лн — явление огибания волнами препятствий, в широком смысле любое отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Ка́устика — огибающая семейства лучей, не сходящихся в одной точке. Каустики в оптике — это особые линии и особые поверхности, вблизи которых резко возрастает интенсивность светового поля.

Эффе́кт Вави́лова — Черенко́ва, эффе́кт Черенко́ва, излуче́ние Вави́лова — Черенко́ва, черенко́вское излуче́ние — свечение, вызываемое в прозрачной среде заряженной частицей, движущейся со скоростью, превышающей фазовую скорость распространения света в этой среде.

Преломле́ние (рефра́кция) — изменение направления луча (волны), возникающее на границе двух сред, через которые этот луч проходит, или в одной среде, но с меняющимися свойствами, в которой скорость распространения волны неодинакова.
Сверхсветово́е движе́ние — движение со скоростью, превышающей скорость света в вакууме. Несмотря на то, что согласно специальной теории относительности скорость света в вакууме является максимально достижимой скоростью распространения сигналов, а энергия частицы положительной массы стремится к бесконечности при приближении её скорости к скорости света, объекты, движение которых не связано с переносом информации, могут иметь сколь угодно большую скорость.
Упру́гие во́лны — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил. При распространении таких волн в среде перемещаются малые упругие колебания.

Звуковой барьер в аэродинамике — название ряда технических трудностей, вызванных явлениями, сопровождающими движение летательного аппарата на скоростях, близких к скорости звука или превышающих её.

Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения в пространстве, вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно. Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта. Её можно рассматривать при желании как векторную величину.
Групповая скорость — это величина, характеризующая скорость распространения «группы волн» — то есть более или менее хорошо локализованной квазимонохроматической волны. Обычно интерпретируется как скорость перемещения максимума амплитудной огибающей квазимонохроматического волнового пакета. В случае рассмотрения распространения волн в пространстве размерностью больше единицы подразумевается, как правило, волновой пакет, близкий по форме к плоской волне.
Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн.

Конус Маха — коническая поверхность, ограничивающая в сверхзвуковом потоке газа область, в которой сосредоточены возмущения, порождённые точечным источником возмущений — телом, обтекаемым потоком или, что эквивалентно, движущимся в среде со сверхзвуковой скоростью; конус Маха разграничивает возмущённую и невозмущённую области среды. Назван в честь Эрнста Маха, который ввёл это понятие в физику.

Вращение плоскости поляризации поперечной волны — физическое явление, заключающееся в повороте поляризационного вектора линейно-поляризованной поперечной волны вокруг её волнового вектора при прохождении волны через анизотропную среду. Волна может быть электромагнитной, акустической, гравитационной и т. д. Линейно-поляризованная поперечная волна может быть описана как суперпозиция двух циркулярно поляризованных волн с одинаковым волновым вектором и амплитудой. В изотропной среде проекции полевого вектора этих двух волн на плоскость поляризации колеблются синфазно, их сумма равна полевому вектору суммарной линейно-поляризованной волны. Если фазовая скорость циркулярно поляризованных волн в среде различна, то одна из волн отстаёт от другой, что приводит к появлению разности фаз между колебаниями указанных проекций на выбранную плоскость. Эта разность фаз изменяется при распространении волны. Если повернуть плоскость поляризации вокруг волнового вектора на угол, равный половине разности фаз, то колебания проекций полевых векторов на неё будут вновь синфазны — повёрнутая плоскость будет плоскостью поляризации в данный момент.
Диспе́рсия волн — в теории волн различие фазовых скоростей линейных волн в зависимости от их частоты. Дисперсия волн приводит к тому, что волновое возмущение произвольной негармонической формы претерпевает изменения (диспергирует) по мере его распространения.

Цилиндри́ческая волна́ — модель волнового процесса, волна, радиально расходящаяся от некоторой прямой в пространстве или сходящаяся к ней. Частным случаем цилиндрической волны на плоскости является круговая волна, расходящаяся от точки.


















