Космическая скорость

Косми́ческие ско́рости (первая v1, вторая v2, третья v3 и четвёртая v4[1]) — характерные критические скорости движения космических объектов в гравитационных полях небесных тел и их систем. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
По определению, космическая скорость — это минимальная начальная скорость, которую необходимо придать объекту (например, космическому аппарату, далее КА) на поверхности небесного тела в отсутствие атмосферы, чтобы:
- v1 — объект стал искусственным спутником центрального тела, то есть стал вращаться по круговой орбите вокруг него на нулевой или пренебрежимо малой высоте относительно поверхности;
- v2 — объект преодолел гравитационное притяжение центрального тела и начал двигаться по параболической орбите, получив тем самым возможность удалиться на бесконечно большое расстояние от него;
- v3 — объект покинул планетную систему, преодолев притяжение планеты и звезды;
- v4 — объект покинул галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Квадрат круговой (первой космической) скорости с точностью до знака равен ньютоновскому потенциалу Φ на поверхности небесного тела (при выборе нулевого потенциала на бесконечности):
где M — масса небесного тела, R — его радиус, G — гравитационная постоянная.
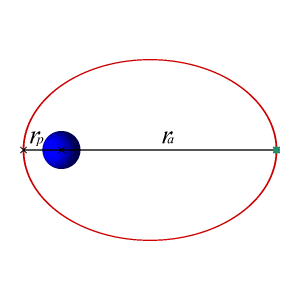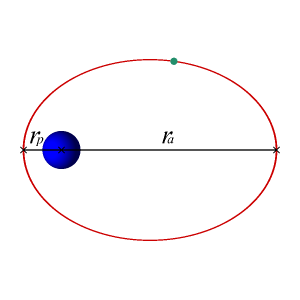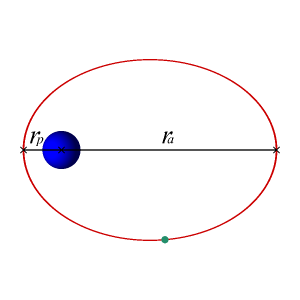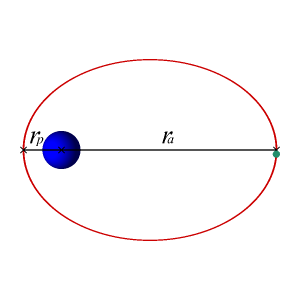
Если скорость КА или другого объекта в момент вывода на орбиту превышает круговую, его орбитой будет эллипс с фокусом в центре притяжения.
Вторая космическая скорость
Между первой и второй космическими скоростями в нерелятивистском случае существует простое соотношение:
Квадрат скорости убегания (второй космической скорости) равен удвоенному ньютоновскому потенциалу на поверхности тела, взятому с обратным знаком:
Вторая космическая скорость (параболическая скорость, скорость убегания) обычно определяется в предположении отсутствия каких-либо других небесных тел. Например, для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Первая и вторая космические скорости для различных небесных тел
| Небесное тело | Масса (по отношению к массе Земли)[2] | v1, км/с[3] | v2, км/с[4] |
|---|---|---|---|
| Энцелад | 1,8×10−5[5] | 0,169 | 0,239[6] |
| Церера | 1,57×10−4[7] | 0,37 | 0,52[6] |
| Луна | 0,0123 | 1,678 | 2,4 |
| Меркурий | 0,0553 | 3,005 | 4,3 |
| Венера | 0,815 | 7,325 | 10,4 |
| Земля | 1 | 7,91 | 11,2 |
| Марс | 0,107 | 3,546 | 5,0 |
| Юпитер | 317,8 | 42,58 | 59,5 |
| Сатурн | 95,2 | 25,535 | 35,5 |
| Уран | 14,54 | 15,121 | 21,3 |
| Нептун | 17,1 | 16,666 | 23,5 |
| Солнце | 332 940 | 437,047 | 618,1[6] |
| Белый карлик Сириус B | 338 933 | 4 800 | 6 800[6] |
| Нейтронная звезда PSR J0348+0432[англ.] | ок. 670 000 | 143 000 ± 10 000[8] | ~ 200 000[8][6] |
Третья космическая скорость
КА, начальная скорость которого не меньше третьей космической скорости, в состоянии преодолеть притяжение Солнца и навсегда покинуть пределы Солнечной системы.
Четвёртая космическая скорость
Четвёртая космическая скорость — минимально необходимая скорость тела, позволяющая преодолеть притяжение галактики в данной точке. Четвёртая космическая скорость используется довольно редко. Ни один искусственный объект пока не развивал такой скорости.
См. также
Примечания
- ↑ Засов А. В., Сурдин В. Г. Космические скорости. Архивная копия от 15 июня 2013 на Wayback Machine
- ↑ Dr. David R. Williams. Planetary Fact Sheet - Ratio to Earth Values (англ.). NASA. Дата обращения: 16 ноября 2017. Архивировано 11 мая 2018 года.
- ↑ Первая космическая скорость, онлайн расчет. Калькулятор – справочный портал. Дата обращения: 26 июля 2019. Архивировано 13 мая 2019 года.
- ↑ Dr. David R. Williams. Planetary Fact Sheet - Metric (англ.). NASA. Дата обращения: 16 ноября 2017. Архивировано 20 августа 2011 года.
- ↑ Jacobson, R. A.; Antreasian, P. G.; Bordi, J. J.; Criddle, K. E. et al. The Gravity Field of the Saturnian System from Satellite Observations and Spacecraft Tracking Data (англ.) // The Astronomical Journal : journal. — IOP Publishing, 2006. — December (vol. 132). — P. 2520—2526. — doi:10.1086/508812.
- ↑ 1 2 3 4 5 Вторая космическая скорость, онлайн расчет. Калькулятор – справочный портал. Дата обращения: 28 июля 2019. Архивировано 13 мая 2019 года.
- ↑ Carry, Benoit; et al. Near-Infrared Mapping and Physical Properties of the Dwarf-Planet Ceres (англ.) // Astronomy and Astrophysics : journal. — EDP Sciences, 2008. — January (vol. 478, no. 1). — P. 235—244. — doi:10.1051/0004-6361:20078166. Архивировано 10 августа 2020 года.
- ↑ 1 2 Строго говоря, при расчёте должны учитываться релятивистские поправки, однако гораздо большую неточность вносит имеющая место на сегодняшний день неопределённость значения радиуса нейтронной звезды
Литература
- Ширмин Г. И. Космические скорости. — 2016. — Кн. Большая российская энциклопедия. Электронная версия.
- Ю. А. Рябов. [bse.sci-lib.com/article065144.html Космические скорости]. — Кн. Большая Советская Энциклопедия (БСЭ).
- Космические скорости / Гл. ред. А. М. Прохоров. — Москва : Советская энциклопедия, 1988. — Кн. Физическая энциклопедия. В 5-ти томах.