Коэффициент Пуассона

Коэффициент Пуассона (обозначается как ${\displaystyle \nu }$, ${\displaystyle \sigma }$ или ${\displaystyle \mu }$) — упругая константа^[1], величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала^[2]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.

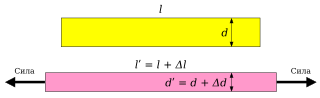
Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях.

Пусть ${\displaystyle l}$ и ${\displaystyle d}$ длина и поперечный размер образца до деформации, а ${\displaystyle l^{\prime }}$ и ${\displaystyle d^{\prime }}$ — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную ${\displaystyle (l^{\prime }-l)}$, а поперечным сжатием — величину, равную ${\displaystyle -(d^{\prime }-d)}$. Если ${\displaystyle (l^{\prime }-l)}$ обозначить как ${\displaystyle \Delta l}$, а ${\displaystyle (d^{\prime }-d)}$ как ${\displaystyle \Delta d}$, то относительное продольное удлинение будет равно величине ${\displaystyle {\frac {\Delta l}{l}}}$, а относительное поперечное сжатие — величине ${\displaystyle -{\frac {\Delta d}{d}}}$. Тогда в принятых обозначениях коэффициент Пуассона ${\displaystyle \mu }$ имеет вид:$${\displaystyle \mu =-{\frac {\Delta d}{d}}{\frac {l}{\Delta l}}}$$Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся ${\displaystyle {\frac {\Delta l}{l}}>0}$ и ${\displaystyle {\frac {\Delta d}{d}}<0}$, так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.

Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5^[3]. Для большинства сплавов, металлов, горных пород значение коэффициента Пуассона лежит в пределах 0,25−0,35, в бетоне 0,16−0,18^[1].

1) Через модуль сдвига ${\displaystyle G}$ и модуль всестороннего сжатия ${\displaystyle K}$$${\displaystyle \sigma ={\frac {1}{2}}{\frac {3K-2G}{3K+G}}}$$2) Через отношение скоростей продольных и поперечных упругих волн^[4]:

$${\displaystyle \sigma ={\frac {\gamma ^{2}-2}{2(\gamma ^{2}-1)}},\quad \gamma ={\frac {V_{P}}{V_{S}}}}$$

Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.

К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы^[5], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0,54), натрий (−0,44), калий (−0,42), кальций (−0,27), медь (−0,13) и других. Простые вещества, образованные 67 % элементов из таблицы Менделеева и имеющие кубическую кристаллическую решетку, имеют отрицательный коэффициент Пуассона.

Коэффициент Пуассона (коэффициент бокового расширения) для грунтов^[6]:

В бентонитовом растворе Коэффициент Пуассона примерно равен 0,5 т.к. в жидкости жесткости E там нет.

• Модуль упругости
• Модуль Юнга