Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Практическое построение окружности возможно с помощью циркуля. Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки, в зависимости от подхода, круг может включать или не включать.

Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Э́ллипс — замкнутая плоская кривая, исторически определённая как одно из конических сечений . Название эллипсу дал Аполлоний Пергский в своей «Конике».
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Эпицикло́ида — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.

Ко́нус — поверхность, образованная в пространстве множеством лучей, соединяющих все точки некоторой плоской кривой с данной точкой пространства.
Логарифми́ческая спира́ль или изогональная спираль — особый вид спирали, часто встречающийся в природе.

Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий, их свойства и связь с другими понятиями определяются аксиомами геометрии.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
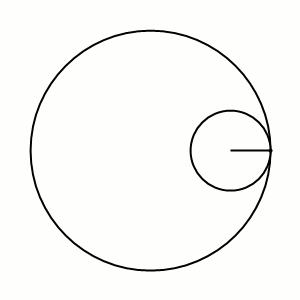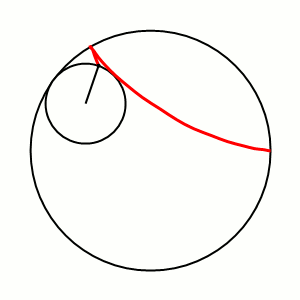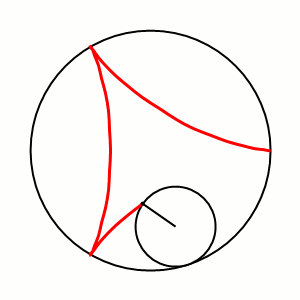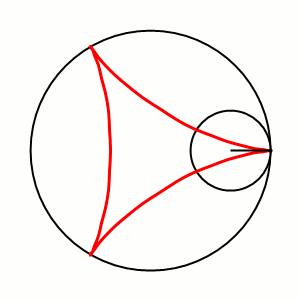
Дельтоида — плоская алгебраическая кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой втрое больше радиуса первой.
Квазитрохоида — — плоская трансцендентная кривая, по форме напоминающая трохоиду, но отличающаяся тем, что центр вращения перемещается по произвольной траектории, радиус и частота вращения могут изменяться во времени по любому закону.

Кривая Персея — сечение тора плоскостью, параллельной оси вращения тора; плоская алгебраическая кривая 4-го порядка. В зависимости от параметров сечения, кривые могут иметь формы «выпуклых» и «вдавленных» овалов, «восьмёрок» и двух овалов.

Циссоида — кривая, созданная из двух заданных кривых C1, C2 относительно точки O (полюса). Пусть L — прямая, проходящая через O и пересекающая C1 в точке P1, а C2 — в точке P2. Пусть P — точка на L такая, что OP = P1P2. Множество таких точек P называется циссоидой кривых C1, C2 относительно O.

Проекция Эккерта IV — это псевдоцилиндрическая картографическая проекция. Полюса представлены как отрезки прямых, длина этих отрезков равна половине длины экватора. Параллели представлены как прямые линии, расположенные через неравные интервалы и уменьшающиеся по длине к полюсам. Меридианы представляют собой эллиптические кривые, расположенные через равные интервалы.

Трисектриса Маклорена — кубика, примечательная своим свойством трисекции, поскольку она может быть использована для трисекции угла. Её можно определить как геометрическое место точек пересечения двух прямых, каждая из которых вращаются равномерно вокруг двух различных точек (полюсов) с отношением угловых скоростей 1:3, при этом первоначально прямые совпадают с прямой, проходящей через эти полюса. Обобщение этого построения называется Секущая Маклорена. Секущая названа в честь Колина Маклорена, который исследовал кривую в 1742 году.

Инверсия кривой — результат применения операции инверсии к заданной кривой C. По отношению к фиксированной окружности с центром O и радиусом k инверсия точки Q — это точка P, лежащая на луче OQ, и OP•OQ = k2. Инверсия кривой C — это множество всех точек P, являющихся инверсиями точек Q, принадлежащих кривой C. Точка O в этом построении называется центром инверсии, окружность называется окружностью инверсии, а k — радиусом инверсии.

Плоская кривая четвёртой степени или плоская квартика — плоская алгебраическая кривая четвёртой степени. Она может быть определена уравнением четвёртой степени от двух переменных:









![{\displaystyle \rho ^{2}=r^{2}-\left[k\sin \theta \pm {\sqrt {c^{2}-k^{2}\cos ^{2}\theta }}\right]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591e1d5770de8100bef38129fed6665f30cd5501)























