Интерполя́ция, интерполи́рование — в вычислительной математике нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору её известных значений, определенным способом. Термин «интерполяция» впервые употребил Джон Валлис в своём трактате «Арифметика бесконечных» (1656).
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез, основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Прогно́з — это научно обоснованное суждение о возможных состояниях объекта в будущем и (или) об альтернативных путях и сроках их осуществления. В узком смысле, это вероятностное суждение о будущем состоянии объекта исследования.

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений, для поиска решения в случае обычных нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
Среднеквадрати́ческое отклонение — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. Обычно означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.
Га́уссовский проце́сс в теории случайных процессов — это вещественный процесс, чьи конечномерные распределения гауссовские.
Геостати́стика — наука и технология для анализа, обработки и представления пространственно-распределенной информации с помощью статистических методов. Геостатистика моделирует распределение объектов, явлений и процессов в географическом пространстве.

Гетероскедасти́чность — понятие, используемое в прикладной статистике, означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.
Линейная регрессия — используемая в статистике регрессионная модель зависимости одной переменной  от другой или нескольких других переменных
от другой или нескольких других переменных  с линейной функцией зависимости.
с линейной функцией зависимости.
Сглаживающий сплайн это метод сглаживания с использованием сплайн-функций.
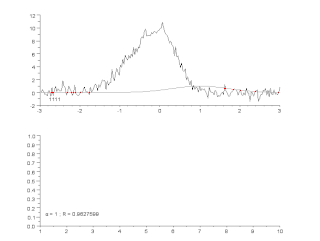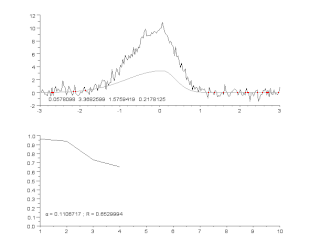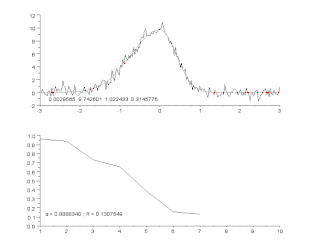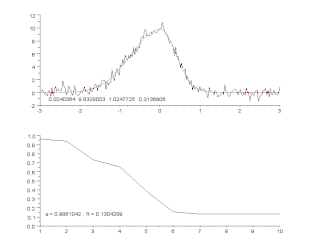
Приближение с помощью кривых — это процесс построения кривой или математической функции, которая наилучшим образом приближается к заданным точкам с возможными ограничениями на кривую. Для построения такого приближения может использоваться либо интерполяция, где требуется точное прохождение кривой через точки, либо сглаживание, когда «сглаживающая» функция проходит через точки приближённо. Связанный раздел — регрессионный анализ, который фокусируется, главным образом, на вопросах статистического вывода, таких как, какая неопределённость заключена в кривой, которая приближает данные с некоторыми случайными ошибками. Построенные кривые могут быть использованы для визуализации данных, для вычисления значений функции в точках, в которых значение не задано и для определения связи между двумя и более переменными. Экстраполяция означает использование полученной кривой за пределами данных, полученных из наблюдения, и порождает некоторую неопределённость, поскольку может зависеть от метода построения кривой.

В статистике регрессия Деминга, названная именем У. К. Деминга, — это вид регрессии с ошибками в переменных, которая пытается найти прямую наилучшего сглаживания для двумерного набора данных. Регрессия отличается от простой линейной регрессии в том, что она принимает во внимание ошибки в наблюдении как по оси x, так и по оси y. Регрессия является частным случаем метода наименьших полных квадратов, которая рассматривает любое число показателей и имеет более сложную структуру ошибок.

Нелинейная регрессия — это вид регрессионного анализа, в котором экспериментальные данные моделируются функцией, являющейся нелинейной комбинацией параметров модели и зависящей от одной и более независимых переменных. Данные аппроксимируются методом последовательных приближений.

В прикладной статистике метод наименьших полных квадратов — это вид регрессии с ошибками в переменных, техника моделирования данных с помощью метода наименьших квадратов, в которой принимаются во внимание ошибки как в зависимых, так и в независимых переменных. Метод является обобщением регрессии Деминга и ортогональной регрессии и может быть применён как к линейным, так и нелинейным моделям.
Обучение признакам или обучение представлениям — это набор техник, которые позволяют системе автоматически обнаружить представления, необходимые для выявления признаков или классификации исходных (сырых) данных. Это заменяет ручное конструирование признаков и позволяет машине как изучать признаки, так и использовать их для решения специфичных задач.

Компромисс отклонение-дисперсия в статистике и в машинном обучении — это свойство набора моделей предсказания, когда модели с меньшим отклонением от имеющихся данных имеют более высокую дисперсию на новых данных, и наоборот. Компромисс отклонение-дисперсия — конфликт при попытке одновременно минимизировать эти два источника ошибки, которые мешают алгоритмам обучения с учителем делать обобщение за пределами тренировочного набора.
- Смещение — это погрешность оценки, возникающая в результате ошибочного предположения в алгоритме обучения. В результате большого смещения алгоритм может пропустить связь между признаками и выводом (недообучение).
- Дисперсия — это ошибка чувствительности к малым отклонениям в тренировочном наборе. При высокой дисперсии алгоритм может как-то трактовать случайный шум в тренировочном наборе, а не желаемый результат (переобучение).

















