Мозаика Пенроуза — общее название трёх особых типов непериодического разбиения плоскости; названы по имени английского математика Роджера Пенроуза, исследовавшего их в 1970-е годы.

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.

Пятиугольный паркет — в геометрии: замощение, составленное из выпуклых пятиугольников. Замощение из правильных пятиугольников в евклидовом пространстве невозможно, поскольку общий угол правильного пятиугольника равен 108° и не делит ни 180°, ни 360°. Однако ими можно замостить гиперболическую плоскость и сферу.
Задача одной плитки — решённая геометрическая проблема поиска одной протоплитки, которая образует непериодическое множество плиток, то есть фигуры, копиями которой можно замостить плоскость, но только непериодичным способом.

Плитки Вана, впервые предложенные математиком, логиком и философом Хао Ваном в 1961, — это класс формальных систем. Они моделируются визуально с помощью квадратных плиток с раскрашиванием каждой стороны. Определяется набор таких плиток, затем копии этих плиток прикладываются друг к другу с условием согласования цветов сторон, но без вращения или симметрического отражения плиток.

В геометрии замощение — это разбиение плоскости на замкнутые множества без промежутков и наложений. Замощение считается периодическим, если существуют параллельные переносы в двух независимых направлениях, которые переносят плитки в точно такие же. Такое замощение состоит из одной фундаментальной единицы или примитивной ячейки, которые повторяются бесконечно в двух независимых направлениях. Пример такого замощения показан на иллюстрации справа. Замощения, которые нельзя построить из единственной примитивной ячейки, называются непериодичными. Если данный набор плиток позволяет только непериодичное замощение, такой набор называется непериодичным.
Мозаика «вертушка» — это непериодичная мозаика, разработанная Чарлзом Радиным и основанная на построении Джона Конвея. Мозаика была первой непериодичной мозаикой, в которой плитки находятся в бесконечном числе различных ориентаций.

Замощение плитками домино области в евклидовой плоскости — мозаика из плиток домино, которые образованы объединением двух единичных квадратов, соединённых по ребру. Эквивалентно — это паросочетание в графе решётки, образованное помещением вершины в центр каждого квадрата области и соединением двух вершин, если два соответствующих квадрата смежны.

Замощения евклидовой плоскости выпуклыми правильными многоугольниками широко использовался ещё с античных времён. Первое систематическое изложение было сделано Кеплером в его книге Harmonices Mundi.

Мозаика Амманна — Бинкера — непериодическая мозаика, которая может быть получена либо с помощью апериодичного множества протоплиток, как это сделал Роберт Амманн в 1970-х годах, либо с помощью метода «вырезать-и-спроецировать», как было сделано независимо Ф. П. М. Бинкером. Поскольку все мозаики, полученные с помощью этих плиток, не периодичны, мозаики Амманна-Бинкера считаются не периодичными. Они входят в пять множеств мозаик, найденных Амманном, и описаны в книге Tilings and Patterns.

Мозаики «гирих» — это набор пяти плиток, использовавшихся для создания орнамента для украшения зданий в исламской архитектуре. Плитки использовались примерно с 12-го века и орнаменты существенно улучшились к моменту построения усыпальницы Дарб-и Имам в городе Исфахан в Иране.

Пифагорова мозаика — замощение евклидовой плоскости квадратами двух различных размеров, в которой каждый квадрат касается четырёх квадратов другого размера своими четырьмя сторонами. Исходя из этой мозаики, можно доказать (наглядно) теорему Пифагора, за что мозаика и получила название пифагоровой. Мозаика часто используется в качестве узора для кафельного пола. В этом контексте мозаика известна также как узор классов.

Гипотеза Келлера — выдвинутая Отт-Генрихом Келлером гипотеза о том, что в любой мозаике в евклидовом пространстве, состоящей из одинаковых гиперкубов, найдутся два куба, соприкасающиеся грань-к-грани. Например, как показано на рисунке, в любой мозаике на плоскости из одинаковых квадратов какие-то два квадрата должны соприкасаться ребро-к-ребру. Перрон доказал, что это верно в размерностях до 6; Бракензик с соавторами доказали верность гипотезы для размерности 7. Однако для бо́льших размерностей это неверно, как показали Лагариас и Шор для размерностей 10 и выше, Макей для размерностей 8 и выше, для чего использовали переформулировку задачи в терминах кликового числа некоторых графов, известных теперь как графы Келлера.

Усечённая квадратная мозаика — полуправильная мозаика из правильных многоугольников на евклидовой плоскости с одним квадратом и двумя восьмиугольниками в каждой вершине. Это единственная мозаика из правильных выпуклых многоугольников, содержащая соприкасающиеся сторонами восьмиугольники. Символ Шлефли мозаики равен t{4,4}.
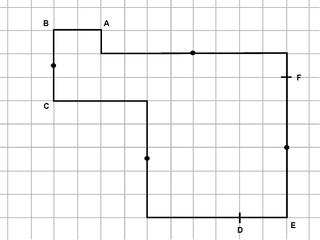
Критерий Конвея — набор условий, при выполнении которых протоплитка замощает плоскость. Назван по имени английского математика Джона Хортона Конвея. Выполнение критерия Конвея является достаточным, но не обязателеным условием для замощения плоскости.
Изоэдральный многогранник размерности 3 или выше — это многогранник, все грани которого одинаковы, также удовлетворяющий некоторым дополнительным ограничениям. Более точно, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны принадлежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела, которая переводит A в B. По этой причине правильные игральные кости имеют форму выпуклых изоэдральных многогранников.

Гирих, а также گره سازی — вид исламского декоративного искусства в архитектуре и художественных ремёслах, состоящий из геометрических линий, образующих переплетённые декоративные орнаменты. В персидской архитектуре орнаменты с узлами можно видеть в кирпичной кладке банна’и, в изделиях из стукко и мозаичных фаянсовых работах. Гирих определяется как «геометрические рисунки, определяемые массивом точек, в которых (прямые) линии пересекаются».

Каирская пятиугольная мозаика является двойственной полуправильной мозаикой на плоскости. Мозаика получила такое название по египетскому городу Каир, улицы которого вымощены такими плитками. Мозаика является одной из 15 известных равногранных пятиугольных мозаик.

Апериодичная мозаика — это непериодичное замощение с дополнительным свойством, что замощение не содержит бесконечно больших периодических кусков. Множество типов плиток является набором непериодичных протоплиток, если копии этих плиток могут образовать только апериодичные мозаики. Мозаики Пенроуза являются наиболее известными примерами апериодичных мозаик.

Плитка Соколара — Тейлор — это одиночная плитка, которая апериодична на плоскости, что означает, что возможны только непериодичные замощения на плоскости при разрешении вращения и зеркального отражения. Плитка была первым примером одиночной апериодичной плитки, или «einstein». Плитка Соколара — Тейлор строится на основе правильного шестиугольника с некоторым узором для обеспечения локального правила соединения. Чтобы реализовать это локальное правило без условий на узор, плитка является несвязной, так как это правило не может быть геометрически реализовано в двухмерном пространстве в виде связной плитки. Из-за этого, для полного решения «Задачи одной плитки» в двумерном пространстве потребовались другие техники.