Куча (структура данных)

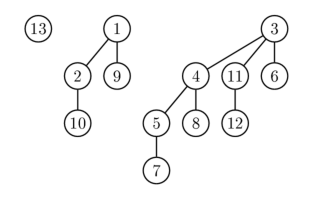
Ку́ча (англ. heap) в программировании — специализированная структура данных типа дерева, которая удовлетворяет свойству кучи: если ${\displaystyle B}$ является узлом-потомком узла ${\displaystyle A}$, то ${\displaystyle k(A)\geqslant k(B)}$, где ${\displaystyle k(X)}$ — ключ (идентификатор) узла. Из этого следует, что элемент с наибольшим значением ключа всегда является корневым узлом кучи, поэтому иногда такие кучи называют max-кучами (в качестве альтернативы, если сравнение перевернуть, то наименьший элемент будет всегда корневым узлом, такие кучи называют min-кучами). Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи, хотя на практике их число обычно не более двух. Куча является максимально эффективной реализацией абстрактного типа данных, который называется очередью с приоритетом. Кучи имеют решающее значение в некоторых эффективных алгоритмах на графах, таких, как алгоритм Дейкстры на d-кучах и сортировка методом пирамиды.

В ранних реализациях Лиспа обеспечивалось динамическое распределение памяти с использованием кучи как структуры данных, впоследствии всякую динамически распределяемую память стали называть «кучей» (хотя она не обязательно использует соответствующую структуру)^[1].

Кучи обычно реализуются в виде массивов, что исключает наличие указателей между её элементами.

Над кучами обычно проводятся следующие операции:

• найти максимум или найти минимум: найти максимальный элемент в max-куче или минимальный элемент в min-куче, соответственно
• удалить максимум или удалить минимум: удалить корневой узел в max- или min-куче, соответственно
• увеличить ключ или уменьшить ключ: обновить ключ в max- или min-куче, соответственно
• добавить: добавление нового ключа в кучу.
• слияние: соединение двух куч с целью создания новой кучи, содержащей все элементы обеих исходных.

В зависимости от ограничений на структуры используются различные варианты куч, некоторые их них:

Различные варианты демонстрируют различную временну́ю сложность вычислений для различных операций^[1] (имена операций в нотации для min-кучи):

Операция	Двоичная	Биномиальная	Фибоначчиева	Спаренная[3]	Бродала
найти минимум	${\displaystyle \Theta (1)}$	${\displaystyle \Theta (\log n)}$ или ${\displaystyle \Theta (1)}$	${\displaystyle \Theta (1)}$[1]	${\displaystyle \Theta (1)}$	${\displaystyle \Theta (1)}$
удалить минимум	${\displaystyle \Theta (\log n)}$	${\displaystyle \Theta (\log n)}$	${\displaystyle O(\log n)}$*	${\displaystyle O(\log n)}$*	${\displaystyle O(\log n)}$
добавить	${\displaystyle \Theta (\log n)}$	${\displaystyle O(\log n)}$	${\displaystyle \Theta (1)}$	${\displaystyle O(1)}$*	${\displaystyle \Theta (1)}$
уменьшить ключ	${\displaystyle \Theta (\log n)}$	${\displaystyle \Theta (\log n)}$	${\displaystyle \Theta (1)}$*	${\displaystyle O(\log n)}$*	${\displaystyle \Theta (1)}$
слияние	${\displaystyle \Theta (n)}$	${\displaystyle O(\log n)}$**	${\displaystyle \Theta (1)}$	${\displaystyle O(1)}$*	${\displaystyle \Theta (1)}$

(*) Амортизированная сложность. В остальных случаях оценка понимается обычным образом: сложность в худшем случае.

(**) ${\displaystyle n}$ — размер наибольшей кучи.

Здесь ${\displaystyle O(F)}$ даёт асимптотическую верхнюю границу, а ${\displaystyle \Theta (F)}$ является асимптотически точной оценкой (в соответствии с нотацией «O» большое и «o» малое).

Структуры данных типа кучи имеют множество применений.

Пирамидальная сортировка: один из лучших применяемых методов сортировки, не имеющий квадратичных наихудших сценариев.

Алгоритмы поиска: при использовании кучи поиск минимума, максимума, того и другого, медианы или k-го наибольшего элемента может быть сделан за линейное время (часто даже за константное время).^[4]

Алгоритмы на графах: применение кучи в качестве структуры данных для внутреннего обхода даёт сокращение времени выполнения на полиномиальный порядок. Примерами таких проблем являются алгоритм построения минимального остовного дерева Прима и проблема кратчайшего пути Дейкстры.

Полная и почти полная бинарная куча может быть представлена очень эффективным способом с помощью индексного массива. Первый (или последний) элемент будет содержать корень. Следующие два элемента массива содержат узлы-потомки корня. Следующие четыре элемента содержат четверых потомков от двух узлов — потомков корня, и так далее. Таким образом, потомки узла уровня n будут расположены на позициях 2n и 2n+1 для массива, индексируемого с единицы, или на позициях 2n+1 и 2n+2 для массива, индексируемого с нуля. Это позволяет перемещаться вверх или вниз по дереву, выполняя простые вычисления индекса массива. Балансировка кучи делается перестановкой элементов, которые нарушают порядок. Поскольку мы можем построить кучу с помощью массива без дополнительной памяти (для узлов, например), то можно использовать пирамидальную сортировку для сортировки массива прямо на месте.

Стандартная библиотека шаблонов языка C++ предоставляет шаблоны функций для управления кучей make_heap, push_heap и pop_heap (обычно реализуются бинарные кучи), которые оперируют с итераторами произвольного доступа. Методы используют итераторы как ссылки на массивы и выполняют преобразование массив-куча.

Набор шаблонов Java платформы Java 2 (начиная с версии 1.5) предоставляет реализацию бинарной кучи в классе java.util.PriorityQueue<E>.

Python имеет модуль heapq, который реализует очереди с приоритетами с помощью бинарной кучи^[5].

Начиная с версии 5.3 PHP в стандартной библиотеке имеются методы maxheap (SplMaxHeap) и minheap (SplMinHeap).

В Perl имеются реализации бинарной, биномиальной и фибоначчиевой кучи во всеобъемлющей сети архивов^[6].