Лемма о руке

Лемма о руке — лемма в доказательстве теоремы Коши о многогранниках.
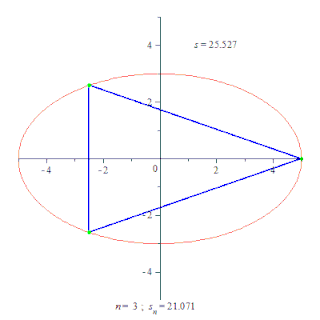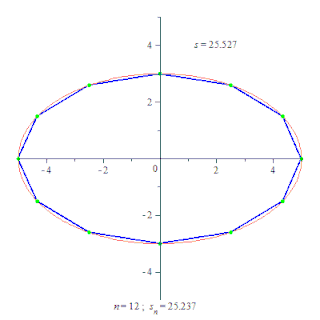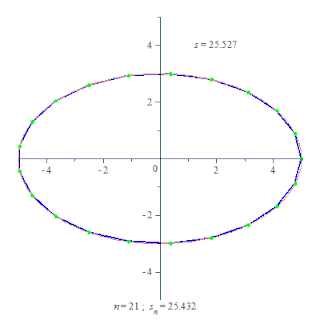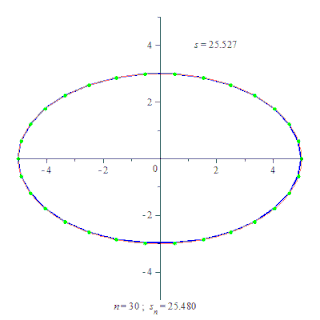
Неформально утверждение можно описать следующим образом: Представьте себе руку робота, состоящую из нескольких звеньев, соединённых суставами. Каждое звено — это отрезок, а вся рука — ломаная. Пусть вся рука робота может двигаться в одной плоскости. Предположим, в изначальном состоянии рука робота образует выпуклую ломаную, то есть такую ломаную, что если мы соединим концы ломаной, то получим выпуклый многоугольник. Допустим теперь, что робот увеличивает угол в каждом суставе. Лемма утверждает, что тогда увеличится и расстояние между началом и концом руки.
Несмотря на простоту формулировки, доказательство леммы не просто. В частности, именно в этом месте оригинальное доказательство Коши имеет ошибку. Эта ошибка оставалась незамеченной более ста лет. Она была замечена Эрнстом Штейницем, видимо, между 1920 и 1928 годами и исправлена только в 1934[1].
Формулировка
Предположим, выпуклый многоугольник на евкидовой плоскости и ломаная в плоскости или пространстве такая, что
- при ,
- при .
Тогда
Более того, в случае равенства ломаные и конгруэнтны.
Вариации и обобщения
- Аналогичный результат верен на сфере и плоскости Лобачевского.
- Более того, лемма естественно обобщается на CAT(κ) пространства.[2]
- Теорема Залгаллера. Если у двух сферических -гольников и соответственные стороны равны и многоугольник лежит в полусфере, то хотя бы один из углов не меньше соответственного угла .[3]
- Лемма о согнутом луке[4] — версия леммы о руке для гладких кривых:
- Пусть и — пара гладких кривых пареметризованных длиной определённых на одном и том же интервале . Предположим, что для любого выполняется неравенство , где и обозначает кривизну и соответственно при . Далее предположим, что есть дуга плоской выпуклой кривой, то есть она проходит вдоль границы некоторой выпуклой плоской фигуры. Тогда расстояние между концами не превосходит расстояния между концаму ; то есть,
- Пусть и — пара гладких кривых пареметризованных длиной определённых на одном и том же интервале . Предположим, что для любого выполняется неравенство , где и обозначает кривизну и соответственно при . Далее предположим, что есть дуга плоской выпуклой кривой, то есть она проходит вдоль границы некоторой выпуклой плоской фигуры. Тогда расстояние между концами не превосходит расстояния между концаму ; то есть,
- Лемма верна если есть кривая в евклидовом пространстве произвольной размерности. Иногда называется леммой Шура в честь Акселя Шур, доказавшего её частный случай.[5] В полной общности лемма была доказана Эрхардом Шмидтом.[6]
См. также
Примечания
- ↑ Steinitz E., Rademacher H. Vorlesungen ̈uber die Theorie der Polyeder. Berlin: Springer-Verl., 1934.
- ↑ см. 9.63 в Alexander, Stephanie; Kapovitch, Vitali; Petrunin, Anton. "Alexandrov geometry: foundations". arXiv:1903.08539v5..
- ↑ В. А. Залгаллер. О деформациях многоугольника на сфере // УМН. — 1956. — Т. 11, № 5(71). — С. 177—178.
- ↑ Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5. Архивировано 11 января 2021 года.
- ↑ Schur, Axel; Über die Schwarzsche Extremaleigenschaft des Kreises unter den Kurven konstanter Krümmung. Math. Ann. 83 (1921), no. 1-2, 143–148.
- ↑ E. Schmidt. «Über das Extremum der Bogenlänge einer Raumkurve bei vorgeschriebenen Einschränkungen ihrer Krümmung». Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. (1925), 485—490.
Литература
- И. Х. Сабитов, Вокруг доказательства леммы Лежандра — Коши о выпуклых многоугольниках Сиб. матем. журн., 2004, том 45, № 4, с. 892—919
- Лекция 24 в Табачников С.Л., Фукс Д.Б. Математический дивертисмент. — МЦНМО, 2011. — ISBN 978-5-94057-731-7.












![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)