
Граф Петерсена — неориентированный граф с 10 вершинами и 15 рёбрами; достаточно простой граф, используемый в качестве примера и контрпримера для многих задач в теории графов.

В теории графов нечётные графы On — это семейство симметричных графов с высоким нечётным обхватом, определённых на некоторых семействах множеств. Они включают и обобщают графы Петерсена.

Граф Грёча — граф без треугольников с 11 вершинами, 20 рёбрами, хроматическим числом 4 и числом скрещиваний 5. Граф назван в честь немецкого математика Герберта Грёча и он демонстрирует необходимость предположения планарности в теореме Грёча, которая утверждает, что любой планарный граф без треугольников можно раскрасить в 3 цвета. Граф Грёча является членом бесконечной последовательности графов без треугольников, в которой каждый граф является мычельскианом предыдущего графа, начиная с нуль-графа. Эта последовательность графов была использована Мыцельским, чтобы показать, что существуют графы без треугольников с произвольно большим хроматическим числом. По этой причине иногда граф Грёча называют графом Мыцельского или Мыцельского-Грёча. В отличие от других, более поздних графов в последовательности, граф Грёча является наименьшим графом без треугольников с его хроматическим числом.

В теории графов колесом Wn называется граф с n вершинами (n ≥ 4), образованный соединением единственной вершины со всеми вершинами (n-1)-цикла. Числовое обозначение колёс в литературе не устоялось — некоторые авторы используют n для обозначения длины цикла, так что их Wn означает граф Wn+1 по определению выше. Колесо может быть определено также, как 1-скелет (n-1)-угольной пирамиды.

Граф Грея — двудольный неориентированный граф с 54 вершинами и 81 рёбрами. Граф является кубическим — любая вершина принадлежит ровно трём рёбрам. Граф был открыт Греем в 1932 году, затем открыт независимо Баувером (Bouwer) в 1968 году в ответ на вопрос, поставленный Фолкманом в 1967 году. Граф Грея примечателен как исторически первый пример кубического графа, имеющего алгебраическое свойство рёберной, но не вершинной транзитивности.

В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества отличаются только одним элементом.

В теории графов снарки «Цветы» образуют бесконечное семейство снарков, введённых Айзексом Руфусом в 1975 году.

Снарк Секереша — снарк с 50 вершинами и 75 рёбрами, пятый известный снарк. Открыт Дьёрдьем Секерешем в 1973 году.

Граф Коксетера — 3-регулярный граф с 28 вершинами и 42 рёбрам Все кубические дистанционно-регулярные графы известны, граф Коксетера — один из 13-ти таких графов.

Граф Вагнера — 3-регулярный граф с 8 вершинами и 12 рёбрами, является 8-вершинной лестницей Мёбиуса.

Полиэдральный граф — неориентированный граф, образованный из вершин и рёбер выпуклого многогранника, или, в контексте теории графов — вершинно 3-связный планарный граф.

Граф Татта — пример кубического полиэдрального графа, не являющегося гамильтоновым. Таким образом, он служит контрпримером к гипотезе Тэйта, предполагавшей, что любой 3-регулярный многогранник имеет гамильтонов цикл.

В теории графов Граф Голднера — Харари — это простой неориентированный граф с 11 вершинами и 27 рёбрами. Файл назван в честь А. Голднера и Ф. Харари, которые в 1975 году доказали, что он является наименьшим негамильтоновым максимальным планарным графом. Тот же самый граф был уже приведён в качестве примера негамильтонова симплициального многогранника Грюнбаумом в 1967.

В теории графов outerplanar graph — это граф, допускающий планарную диаграмму, в которой все вершины принадлежат внешней грани.

Панциклический граф — ориентированный или неориентированный граф, который содержит циклы всех возможных длин от трёх до числа вершин графа. Панциклические графы являются обобщением гамильтоновых графов, графов, которые имеют циклы максимальной возможной длины.
Граф призмы — рёберный граф одной из призм.

Граф дружеских отношений Fn — это планарный неориентированный граф с 2n+1 вершинами и 3n рёбрами.

Алмаз — планарный неориентированный граф с 4 вершинами и 5 рёбрами. Граф представляет собой полный граф  без одного ребра.
без одного ребра.

Граф Мередита — 4-регулярный неориентированный граф с 70 вершинами и 140 рёбрами, обнаруженный Гаем Мередитом в 1973 году.

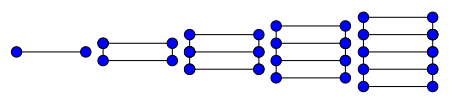
 Хроматическое число лестницы равно 2.
Хроматическое число лестницы равно 2.
























