Линейная булева функция

Линейная булева функция — булева функция, полином Жегалкина которой имеет первую степень.^[1] Более развёрнуто булева функция $f(x_{1},\ldots ,x_{2})$ называется линейной, если она выражается в виде:

f(x_{1},\ldots ,x_{n})=a_{1}x_{1}\oplus \ldots \oplus a_{n}x_{n}\oplus a_{0}

Примеры линейных булевых функций: тождественный $0$ , тождественная $1$ , тождественная функция, отрицание, исключающее или, эквиваленция. Конъюнкция и дизъюнкция линейными не являются.

Количество линейных функций $n$ переменных равно $2^{n+1}$ . Переменная $x_{i}$ линейной функции существенна тогда и только тогда, когда $a_{i}=1$ .

Линейные функции допускают также двойственное определение. Булева функция является линейной тогда и только тогда, когда её кополином Жегалкина имеет первую степень. Линейные функции легко переводятся между представлениями в виде полинома и кополинома при помощи следующих свойств:

$x\leftrightarrow y=x\oplus y\oplus 1$
$x\oplus y=x\leftrightarrow y\leftrightarrow 0$

Множество всех линейных булевых функций образует замкнутый класс, предполный в $P_{2}$ . Таким образом, класс линейных функций является одним из пяти предполных классов булевой логики.

Функция является линейной тогда и только тогда, когда значения функции на любых двух соседних по существенной переменной наборах отличаются. У любой линейной функции равное количество нулей и единиц.

См. также

Примечания

↑ Капитонова, Кривой, Летичевский, 2004.

Литература

Капитонова Ю. В., Кривой С. Л., Летичевский А. А. Лекции по дискретной математике. — СПб.: БХВ-Петербург, 2004. — С. 112. — ISBN 5-94157-546-7.
Couceiro, Miguel; Lehtonen, Erkko (Aug 2020). Linearly definable classes of Boolean functions. ALGOS 2020 - 1st International Conference on Algebras, Graphs and Ordered Sets. Nancy, France.
Filmus, Yuval (Published 13 December 2021). "Boolean Functions on Sn Which Are Nearly Linear". DISCRETE ANALYSIS. 2021 (25): 27. {{cite journal}}: Проверьте значение даты: |date= ()

Похожие исследовательские статьи

Алгебра логики — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики.

Систе́ма аксио́м Це́рмело — Фре́нкеля (ZF) — наиболее широко используемый вариант аксиоматической теории множеств, являющийся фактическим стандартом для оснований математики. Сформулирована Эрнстом Цермело в 1908 году как средство преодоления парадоксов теории множеств, и уточнена Абрахамом Френкелем в 1921 году.

Дифференци́руемая фу́нкция — это функция, у которой существует дифференциал. Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Опера́тор — математическое отображение между множествами, в котором каждое из них наделено какой-либо дополнительной структурой. Понятие оператора используется в различных разделах математики для отличия от другого рода отображений ; точное значение зависит от контекста, например в функциональном анализе под операторами понимают отображения, ставящие в соответствие функции другую функцию.

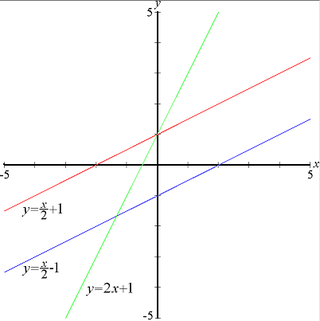
Линейная функция — функция вида

\text{[math]}

Булева формула — терм над некоторым множеством булевых функций. Более развёрнуто: пусть $\text{[math]}$ — некоторое множество булевых функций, $\text{[math]}$ — множество символов переменных, $\text{[math]}$ « $\text{[math]}$ » « $\text{[math]}$ » « $\text{[math]}$ » $\text{[math]}$ — множество символов пунктуации, причём все три множества попарно непересекаются. Булева формула над множеством функций $\text{[math]}$ и множеством переменных $\text{[math]}$ индуктивно определяется как слово над алфавитом $\text{[math]}$ следующим образом:

слово $\text{[math]}$ , где $\text{[math]}$ — формула;
слово $\text{[math]}$ , где $\text{[math]}$ и $\text{[math]}$ имеет арность $\text{[math]}$ — формула;
слово $\text{[math]}$ , где $\text{[math]}$ , $\text{[math]}$ имеет арность $\text{[math]}$ , $\text{[math]}$ — некоторые формулы, — формула;
любая формула получена за конечное число применения шагов 1-3.

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Замкнутый класс в теории булевых функций — такое множество $\text{[math]}$ функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: $\text{[math]}$ . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества $\text{[math]}$ , снова входит в это же множество.

Критерий Поста — одна из центральных теорем в теории булевых функций, устанавливающая необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию. Впервые сформулирован американским математиком Эмилем Постом.

Бу́лева фу́нкция от $\text{[math]}$ аргументов — в дискретной математике — отображение $\text{[math]}$ , где $\text{[math]}$ — булево множество. Элементы булева множества $\text{[math]}$ обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число $\text{[math]}$ , обозначающее количество аргументов, называется арностью или местностью функции, в случае $\text{[math]}$ булева функция превращается в булеву константу. Элементы декартова произведения $\text{[math]}$ называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается $\text{[math]}$ , а от $\text{[math]}$ аргументов — $\text{[math]}$ . Переменные, принимающие значения из булева множества, называются булевыми переменными. Булевы функции названы по фамилии математика Джорджа Буля.

Предполный класс в теории булевых функций — замкнутый класс булевых функций, обладающий следующим свойством — замыкание объединения этого класса с любой булевой функцией, не принадлежащей ему, порождает все $\text{[math]}$ . Множество предполных классов булевых функций исчерпывается списком:

Класс $\text{[math]}$ функций, сохраняющих константу 0:
$\text{[math]}$ .
Класс $\text{[math]}$ функций, сохраняющих константу 1:
$\text{[math]}$ .
Класс $\text{[math]}$ самодвойственных функций:
$\text{[math]}$ .
Класс $\text{[math]}$ монотонных функций:
$\text{[math]}$ .
Класс $\text{[math]}$ линейных функций — представимых полиномом Жегалкина первой степени:
$\text{[math]}$ .

Полином Жегалкина — многочлен над полем $\text{[math]}$ , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).

Самодвойственная функция — булева функция, двойственная сама к себе. Более развёрнуто, булева функция $\text{[math]}$ называется самодвойственной, если для любых значений $\text{[math]}$ верно

\text{[math]}

BelT — государственный стандарт симметричного шифрования и контроля целостности Республики Беларусь. Полное название стандарта — СТБ 34.101.31-2007 «Информационные технологии и безопасность. Криптографические алгоритмы шифрования и контроля целостности». Принят в качестве предварительного стандарта в 2007 году. Введен в действие в качестве окончательного стандарта в 2011 году.

Бинарная диаграмма решений (БДР) или "программа с ветвлением" является формой представления булевой функции $\text{[math]}$ от $\text{[math]}$ переменных в виде направленного ациклического графа, состоящего из внутренних узлов решений, каждый из которых имеет по два потомка, и двух терминальных узлов, каждый из которых соответствует одному из двух значений булевой функции. В зарубежной литературе бинарные диаграммы решений и программы с ветвлением называются binary decision diagram (BDD) и branching programs (BP) соответственно.

Функциональная полнота множества логических операций или булевых функций — это возможность выразить все возможные значения таблиц истинности с помощью формул из элементов этого множества. Математическая логика обычно использует такой набор операций: конъюнкция, дизъюнкция, отрицание, импликация и эквиваленция. Это множество операций является функционально полным. Но оно не является минимальной функционально полной системой, поскольку:

\text{[math]}

\text{[math]}

Бент-функция — булева функция с чётным числом переменных, для которой расстояние Хэмминга от множества аффинных булевых функций с тем же числом переменных максимально. Бент-функции в этом смысле обладают максимальной степенью нелинейности среди всех функций с данным числом переменных и благодаря этому широко применяются в криптографии для создания шифров, максимально устойчивых к методам линейного и дифференциального криптоанализа.

Алгебра Жегалкина — множество булевых функций, на котором определены нульарная операция взятия единицы $\text{[math]}$ , бинарная операция конъюнкции $\text{[math]}$ и бинарная операция суммы по модулю два $\text{[math]}$ . Константа ноль вводится как $\text{[math]}$ . Операция отрицания вводится соотношением $\text{[math]}$ . Операция дизъюнкции следует из тождества $\text{[math]}$ .

Монотонная булева функция — булева функция, которая монотонно возрастает по каждому аргументу. Класс всех монотонных булевых функций является одним из пяти предполных классов.

Двойственная булева функция к булевой функции $\text{[math]}$ — функция $\text{[math]}$ , определяемая соотношением

\text{[math]}

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.