Магнитное поле Земли

Магни́тное по́ле Земли́ или геомагни́тное по́ле — магнитное поле, генерируемое внутриземными источниками. Предмет изучения геомагнетизма. Появилось 4,2 млрд лет назад^[1].

Собственное магнитное поле Земли (геомагнитное поле) можно разделить на cледующие основные части^[2]:

• главное поле,
• поля мировых аномалий,
• внешнее магнитное поле.

Более чем на 90 % оно состоит из поля, источник которого находится внутри Земли, в жидком внешнем ядре, — эта часть называется главным, основным или нормальным полем^[3][4][5]. Оно аппроксимируется в виде ряда по гармоникам — ряда Гаусса, а в первом приближении вблизи поверхности Земли (до трёх её радиусов) близко к полю магнитного диполя, то есть имеет такой вид, как будто земной шар представляет собой полосовой магнит с осью, направленной приблизительно с севера на юг^{[2][3][6][7][8]}. Центр этого диполя смещен относительно центра Земли, а ось наклонена к оси вращения Земли на угол около 10°. На такой же угол отстоят от соответствующих географических полюсов геомагнитные полюса — точки пересечения оси диполя с поверхностью Земли^[4]. Их положение в различные моменты времени вычисляется в рамках той или иной модели магнитного поля, определяющей тем или иным образом первые три коэффициента в ряду Гаусса^[3]. Эти глобальные модели, такие как Международное геомагнитное аналитическое поле (International Geomagnetic Reference Field, IGRF)^[9] и Всемирная магнитная модель (World Magnetic Model, WMM)^{[англ.][10]}, создаются различными международными геофизическими организациями, и каждые 5 лет утверждаются и публикуются обновлённые наборы коэффициентов Гаусса, определяющих все данные о состоянии геомагнитного поля и его параметрах^[4]. Так, согласно модели WMM2015, Северный геомагнитный полюс (по сути это южный полюс магнита) имеет координаты 80,37° с. ш. и 72,62° з. д., Южный геомагнитный полюс — 80,37° ю. ш., 107,38° в. д., наклон оси диполя относительно оси вращения Земли — 9,63°^[3][11]. Перпендикулярная магнитной оси окружность поверхности Земли, на которой чётко сбалансированная магнитная стрелка останется абсолютно горизонтальной, называется магнитным экватором.

Реальные силовые линии магнитного поля Земли, хотя в среднем и близки к силовым линиям диполя, отличаются от них местными нерегулярностями, связанными с наличием намагниченных пород в коре, расположенных близко к поверхности. Из-за этого в некоторых местах на земной поверхности параметры поля сильно отличаются от значений в близлежащих районах, образуя так называемые магнитные аномалии^[2][4][7][8]. Они могут накладываться одна на другую, если вызывающие их намагниченные тела залегают на разных глубинах^[5].

Существование магнитных полей протяжённых местных областей внешних оболочек Земли приводит к тому, что истинные магнитные полюса — точки (вернее, небольшие области), в которых силовые линии магнитного поля абсолютно вертикальны, — не совпадают с геомагнитными, при этом они лежат не на самой поверхности Земли, а под ней^[3][4][6]. Координаты магнитных полюсов на тот или иной момент времени также вычисляются в рамках различных моделей геомагнитного поля путём нахождения итеративным методом всех коэффициентов в ряду Гаусса. Так, согласно актуальной модели WMM, в 2015 г. Северный магнитный полюс находился в точке 86° с. ш., 159° з. д., а южный — 64° ю. ш., 137° в.д^[3]. Значения актуальной модели IGRF12 немного отличаются: 86,3° с. ш., 160° з. д. для Северного магнитного полюса, 64,3° ю. ш., 136,6° в.д для Южного^[11].

Соответственно, магнитная ось — прямая, проходящая через магнитные полюса, — не проходит через центр Земли и не является её диаметром^[6][7]. Это означает, что магнитные полюса, в отличие от географических, не являются антиподами.

Положения всех полюсов постоянно смещаются — геомагнитный полюс прецессирует относительно географического с периодом около 1200 лет^[2].

В начале XXI века скорость смещения Северного магнитного полюса увеличилась с 15 км/год до 55 км/год (2 мм/с)^[12]

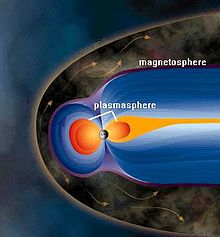
Оно определяется источниками в виде токовых систем, находящимися за пределами земной поверхности, в её атмосфере^[2][4]. В верхней части атмосферы (100 км и выше) — ионосфере — её молекулы ионизируются, формируя плотную холодную плазму, поднимающуюся выше, поэтому часть магнитосферы Земли выше ионосферы, простирающаяся на расстояние до трёх её радиусов, называется плазмосферой. Плазма удерживается магнитным полем Земли, но её состояние определяется его взаимодействием с солнечным ветром — потоком плазмы солнечной короны^[13].

Таким образом, на большем удалении от поверхности Земли магнитное поле несимметрично, так как искажается под действием солнечного ветра: со стороны Солнца оно сжимается, а в направлении от Солнца приобретает «шлейф», который простирается на сотни тысяч километров, выходя за орбиту Луны^[2]. Эта своеобразная «хвостатая» форма возникает, когда плазма солнечного ветра и солнечных корпускулярных потоков как бы обтекают земную магнитосферу — область околоземного космического пространства, ещё контролируемую магнитным полем Земли, а не Солнца и других межпланетных источников^[2][4][7][8]; она отделяется от межпланетного пространства магнитопаузой, где динамическое давление солнечного ветра уравновешивается давлением собственного магнитного поля. Подсолнечная точка магнитосферы в среднем находится на расстоянии 10 земных радиусов R_⊕; при слабом солнечном ветре это расстояние достигает 15—20 R_⊕, а в период магнитных возмущений на Земле магнитопауза может заходить за геостационарную орбиту (6,6 R_⊕)^[2]. Вытянутый хвост на ночной стороне имеет диаметр около 40 R_⊕ и длину более 900 R_⊕; начиная с расстояния примерно 8 R_⊕, он разделен на части плоским нейтральным слоем, в котором индукция поля близка к нулю^[2][4][7][8].

Геомагнитное поле вследствие специфической конфигурации линий индукции создает для заряженных частиц — протонов и электронов — магнитную ловушку. Оно захватывает и удерживает огромное их количество, так что магнитосфера является своеобразным резервуаром заряженных частиц. Общая их масса, по различным оценкам, составляет от 1 кг до 10 кг. Они формируют так называемый радиационный пояс, охватывающий Землю со всех сторон, кроме приполярных областей. Его условно разделяют на два — внутренний и внешний. Нижняя граница внутреннего пояса находится на высоте около 500 км, его толщина — несколько тысяч километров. Внешний пояс находится на высоте 10—15 тыс. км. Частицы радиационного пояса под действием силы Лоренца совершают сложные периодические движения из Северного полушария в Южное и обратно, одновременно медленно перемещаясь вокруг Земли по азимуту. В зависимости от энергии они совершают полный оборот вокруг Земли за время от нескольких минут до суток^[7].

Магнитосфера не подпускает к земле потоки космических частиц^[8]. Однако в её хвосте, на больших расстояниях от Земли напряженность геомагнитного поля, а следовательно, и его защитные свойства, ослабляются, и некоторые частицы солнечной плазмы получают возможность попасть вовнутрь магнитосферы и магнитных ловушек радиационных поясов. Хвост таким образом служит местом формирования потоков высыпающихся частиц, вызывающих полярные сияния и авроральные токи^[2]. В полярных областях часть потока солнечной плазмы вторгается в верхние слои атмосферы из радиационного пояса Земли и, сталкиваясь с молекулами кислорода и азота, возбуждает их или ионизирует, а при обратном переходе в невозбужденное состояние атомы кислорода излучают фотоны с λ = 0,56 мкм и λ = 0,63 мкм, ионизированные же молекулы азота при рекомбинации высвечивают синие и фиолетовые полосы спектра. При этом наблюдаются полярные сияния, особенно динамичные и яркие во время магнитных бурь. Они происходят при возмущениях в магнитосфере, вызванных увеличением плотности и скорости солнечного ветра при усилении солнечной активности^[7][8].

Наглядное представление о положении линий магнитной индукции поля Земли даёт магнитная стрелка, закреплённая таким образом, что может свободно вращаться и вокруг вертикальной, и вокруг горизонтальной оси (например, в кардановом подвесе), — в каждой точке вблизи поверхности Земли она устанавливается определённым образом вдоль этих линий.

Поскольку магнитные и географические полюса не совпадают, магнитная стрелка указывает направление с севера на юг только приблизительно. Вертикальную плоскость, в которой устанавливается магнитная стрелка, называют плоскостью магнитного меридиана данного места, а линию, по которой эта плоскость пересекается с поверхностью Земли, — магнитным меридианом^[6][8]. Таким образом, магнитные меридианы — это проекции силовых линий магнитного поля Земли на её поверхность, сходящиеся в Северном и Южном магнитных полюсах^[14]. Угол между направлениями магнитного и географического меридианов называют магнитным склонением. Оно может быть западным (часто обозначается знаком «−») или восточным (знак «+») в зависимости от того, к западу или востоку отклоняется северный полюс магнитной стрелки от вертикальной плоскости географического меридиана^[6][7][8].

Далее, линии магнитного поля Земли, вообще говоря, не параллельны её поверхности. Это означает, что магнитная индукция поля Земли не лежит в плоскости горизонта данного места, а образует с этой плоскостью некий угол — он называется магнитным наклонением^[6][8]. Оно близко к нулю лишь в точках магнитного экватора — окружности большого круга в плоскости, которая перпендикулярна к магнитной оси^[3].

Магнитное склонение и магнитное наклонение определяют направление магнитной индукции поля Земли в каждом конкретном месте. А численное значение этой величины можно найти, зная наклонение и одну из проекций вектора магнитной индукции ${\displaystyle \mathbf {B} }$ — на вертикальную или горизонтальную ось (последнее оказывается более удобным на практике). Таким образом, три этих параметра — магнитное склонение, наклонение и модуль вектора магнитной индукции B (либо вектора напряжённости магнитного поля ${\displaystyle \mathbf {H} }$) — полностью характеризуют геомагнитное поле в данном месте. Их точное знание для максимально большого числа пунктов на Земле имеет чрезвычайно важное значение^[6][8]. Составляются специальные магнитные карты, на которых нанесены изогоны (линии одинакового склонения) и изоклины (линии одинакового наклонения), необходимые для ориентации с помощью компаса^[8].

В среднем интенсивность магнитного поля Земли колеблется от 25 до 65 мкТл (0,25—0,65 Гс) и сильно зависит от географического положения^[3]. Это соответствует средней напряжённости поля около 0,5 Э (40 А/м)^[2]. На магнитном экваторе её величина около 0,34 Э, у магнитных полюсов — около 0,66 Э. В некоторых районах (магнитных аномалий) напряжённость резко возрастает: в районе Курской магнитной аномалии она достигает 2 Э^[7].

Магнитный дипольный момент Земли на 2015 год составлял 7,72⋅10²⁵ Гс·см³ (или 7,72⋅10²² А·м²), уменьшаясь в среднем за последние десятилетия на 0,007⋅10²⁵ Гс·см³ в год^[11].

Впервые объяснить существование магнитных полей Земли и Солнца попытался Дж. Лармор в 1919 году^[19], предложив концепцию динамо, согласно которой поддержание магнитного поля небесного тела происходит под действием гидродинамического движения электропроводящей среды. Однако в 1934 году Т. Каулинг^{[англ.][20]} доказал теорему о невозможности поддержания осесимметричного магнитного поля посредством гидродинамического динамо-механизма. А поскольку большинство изучаемых небесных тел (и тем более Земля) считались аксиально-симметричными, на основании этого можно было сделать предположение, что их поле тоже будет аксиально-симметричным, и тогда его генерация по такому принципу будет невозможна согласно этой теореме^[21]. Даже Альберт Эйнштейн скептически относился к осуществимости такого динамо при условии невозможности существования простых (симметричных) решений. Лишь гораздо позже было показано, что не у всех уравнений с аксиальной симметрией, описывающих процесс генерации магнитного поля, решение будет аксиально-симметричным, и в 1950-х гг. несимметричные решения были найдены^[16][21].

С тех пор теория динамо успешно развивается, и на сегодняшний день общепринятым, наиболее вероятным объяснением происхождения магнитного поля Земли и других планет, является самовозбуждающийся динамо-механизм, основанный на генерации электрического тока в проводнике при его движении в магнитном поле, порождаемом и усиливаемом самими этими токами. Необходимые условия создаются в ядре Земли: в жидком внешнем ядре, состоящем в основном из железа при температуре порядка 4—6 тысяч кельвин, которое отлично проводит ток, создаются конвективные потоки, отводящие от твёрдого внутреннего ядра тепло (генерируемое благодаря распаду радиоактивных элементов либо освобождению скрытой теплоты при затвердевании вещества на границе между внутренним и внешним ядром по мере постепенного остывания планеты). Силы Кориолиса закручивают эти потоки в характерные спирали, образующие так называемые столбы Тейлора^[англ.]. Благодаря трению слоёв они приобретают электрический заряд, формируя контурные токи. Таким образом, создаётся система токов, циркулирующих по проводящему контуру в движущихся в (изначально присутствующем, пусть и очень слабом) магнитном поле проводниках, как в диске Фарадея. Она создает магнитное поле, которое при благоприятной геометрии течений усиливает начальное поле, а это, в свою очередь, усиливает ток, и процесс усиления продолжается до тех пор, пока растущие с увеличением тока потери на джоулево тепло не уравновесят притоки энергии, поступающей за счет гидродинамических движений^{[15][17][22][23]}. Высказывались предположения, что динамо может возбуждаться за счёт прецессии или приливных сил, то есть что источником энергии является вращение Земли, однако наиболее распространена и разработана гипотеза о том, что это всё же именно термохимическая конвекция^[18].

Математически этот процесс описывается магнитогидродинамическим уравнением индукции^{[англ.][17][18][24]}

${\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {\nabla } \times (\mathbf {u} \times \mathbf {B} )+\eta \mathbf {\nabla } ^{2}\mathbf {B} }$,

где u — скорость потока жидкости, B — магнитная индукция, η = 1/μσ — магнитная вязкость^[англ.] (коэффициент магнитной диффузии), σ — электропроводность жидкости, а μ — магнитная проницаемость, практически не отличающаяся при такой высокой температуре ядра от μ₀ — проницаемости вакуума. Первое слагаемое в правой части соответствует формированию магнитного поля, а второе — его подавлению. При u=0 (без динамо) решение этого уравнения — поле, полностью угасающее через 6⋅10⁴ лет^[24].

Однако для полного описания необходимо записать систему магнитогидродинамических уравнений. В приближении Буссинеска (в рамках которого пренебрегается т. н. вековым охлаждением и все физические характеристики жидкости полагаются постоянными, кроме силы Архимеда, при расчёте которой учитываются изменения плотности вследствие разности температур и — в общем случае — концентрации лёгких элементов) это^[17][18][24]:

• Уравнение Навье — Стокса, содержащее члены, выражающие совокупное действие вращения и магнитного поля:

${\displaystyle \rho _{0}\left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \mathbf {u} \right)=-\nabla P+\rho _{0}\nu \mathbf {\nabla } ^{2}\mathbf {u} +\rho {\bar {\mathbf {g} }}-2\rho _{0}\mathbf {\Omega } \times \mathbf {u} +\mathbf {J} \times \mathbf {B} }$.

Здесь ρ — плотность, ν — кинематическая вязкость, ${\displaystyle P=p-{\frac {\rho _{0}}{2}}|\mathbf {\Omega } \times \mathbf {r} |^{2}}$ — «эффективное» давление с учётом центробежной силы (хотя в некоторых моделях она полагается пренебрежимо малой), ${\displaystyle {\bar {\mathbf {g} }}=g_{0}{\frac {\mathbf {r} }{R_{0}}}}$ — сила тяготения (R₀ — радиус внешнего ядра), Ω — угловая скорость вращения мантии, полагаемая равной скорости вращения внутреннего ядра, ${\displaystyle \mathbf {J} ={\frac {1}{\mu }}\nabla \times \mathbf {B} }$ — плотность тока согласно закону Ампера, индекс «0» всюду обозначает значения на границе внешнего ядра. Левая часть уравнения — производная от импульса на единицу объёма, то есть производная по времени от величины ρ₀V, увлекаемой движением жидкости; правая часть — сумма сил, вызывающих это изменение импульса: градиент давления^[англ.], вязкость, гравитация (сила Архимеда), вращение (сила Кориолиса) и магнитное поле (сила Лоренца)^[17].

Вращение Земли — один из важнейших факторов формирования геомагнитного поля, и его механизм схож с процессами в атмосфере Земли, приводящим к завихрению воздушных масс против часовой стрелки в Северном полушарии и в обратном направлении в Южном — циклонам и антициклонам. Аналогичные завихрения конвекционных потоков в ядре приводят к тому, что отдельные турбулентные конвекционные движения приобретают крупномасштабную (при усреднении по пульсациям скорости) зеркальную асимметрию и в совокупности приводят к генерации динамо в макроскопических масштабах благодаря электродвижущей силе, направленной уже вдоль, а не перпендикулярно среднему (которое определяется усреднением реального поля по его возможным статистическим реализациям) магнитному полю ${\displaystyle \langle \mathbf {\varepsilon } \rangle =\alpha \langle \mathbf {B} \rangle }$, где ε — ЭДС, а α — коэффициент пропорциональности, из-за которого этот механизм и получил название альфа-эффект^[23][25]. В общем случае α — тензор, однако зеркальная антисимметрия даёт псевдоскаляр, которого и требует по построению эта формула, так как ε — истинный вектор, а B — псевдовектор^[26]. Динамо, основанное исключительно на α-эффекте, называют α²-динамо, поскольку его действие выражается произведением двух членов, содержащих этот коэффициент^[24], — оно характеризуется практически стационарным полем, испытывающим небольшие кратковременные вариации (порядка сотен лет для Земли) и долговременные полные инверсии (порядка миллиона лет для Земли). Возможен также механизм с действием омега-эффекта (более существенного для Солнца, чем для Земли, однако необходимого для объяснения природы наблюдаемого дрейфа геомагнитных неоднородностей) — это измеряемое градиентом скорости дифференциальное вращение, которое из направленного к наблюдателю полоидального (вытянутого вдоль меридианов, B_S) магнитного поля создаёт скрытое в проводящем ядре планеты тороидальное (вытянутое вдоль параллелей, B_T) поле. Альфа-эффект замыкает цикл генерации — превращая тороидальное поле в полоидальное за счёт вихрей, характеризуемых отрицательной спиральностью (эта характеристика выражается соотношением ${\displaystyle \mathbf {u} \cdot \mathbf {\nabla } \times \mathbf {u} }$ и непосредственно связана с величиной α) в Северном полушарии и положительной в Южном: восходящие и нисходящие потоки в конвекционных цилиндрах вытягивают и поворачивают B_T-линии в S-направлении^{[16][18][21][27]}. Такая схема обычно называется αω-эффектом, она даёт переменные поля, и при этом B_T>>B_S, тогда как для α²-механизма эти компоненты сравнимы (экспериментально на сегодняшний день удалось получить только грубую оценку |B_S|<|B_T|<100|B_S|). И если источником полоидального поля может быть только альфа-эффект, то тороидального — оба, причём если оба вносят существенный вклад, соответствующий механизм иногда обозначают α²ω. Большинство теоретических моделей магнитного динамо — типа α². В обоих случаях, как альфа, так и омега-эффектов, таким образом снимаются ограничения теоремы Каулинга^[17][24]. Однако существует ряд геометрий течений, для которых динамо также невозможно (например, чисто тороидальное поле скоростей^[24][28]), в то же время при определённых условиях оно возможно и при нулевой суммарной завихрённости ${\displaystyle \mathbf {\nabla } \times \mathbf {u} }$ и нулевой спиральности; возможны и другие эффекты, приводящие к возникновению ЭДС, параллельной магнитному полю^[26].

• Уравнение теплопроводности, выражающее закон сохранения энергии:

${\displaystyle {\frac {\partial T}{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } T=\kappa \mathbf {\nabla } ^{2}T+\epsilon }$,

где T — температура, κ = k/(ρc_p) — температуропроводность (коэффициент тепловой диффузии), k — теплопроводность, c_p — удельная теплоёмкость среды при постоянном давлении. Последнее слагаемое, ε, пропорционально выделению тепла, генерируемого теми или иными растворёнными в жидкости источниками (такими как радиоактивный распад), на единицу массы. В моделях, учитывающих перенос не только тепла, но и вещества, записывается соответствующее аналогичное уравнение относительно переменной ξ — массовой доли лёгких элементов (считается, что это сера и кислород) в составе ядра:

${\displaystyle {\frac {\partial \xi }{\partial t}}+\mathbf {u} \cdot \mathbf {\nabla } \xi =\kappa _{\xi }\mathbf {\nabla } ^{2}\xi +\epsilon _{\xi }}$,

где κ_ξ — коэффициент (молекулярной) диффузии. В большинстве моделей динамо, однако для простоты разность температур и концентраций лёгких элементов объединяются в одну отвечающую за плавучесть переменную.

• Уравнение непрерывности:

${\displaystyle \mathbf {\nabla } \cdot \mathbf {u} =0}$.

• Также должна выполняться теорема Гаусса

${\displaystyle \mathbf {\nabla } \cdot \mathbf {B} =0}$.

• Наконец, уравнение состояния; в различных моделях используются различные его формы, например,

${\displaystyle \rho =\rho _{0}\left[1-\alpha (T-T_{0})\right]}$,

где α — коэффициент линейного теплового расширения (обозначение совпадает с коэффициентом пропорциональности в уравнении для альфа-эффекта). В общем случае, при учёте массопереноса, в квадратных скобках присутствует также слагаемое ${\displaystyle \alpha _{\xi }(\xi -\xi _{0})}$. Здесь ${\displaystyle \alpha =-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial T}}\right)_{P,\xi }}$, ${\displaystyle \alpha _{\xi }=-{\frac {1}{\rho }}\left({\frac {\partial \rho }{\partial \xi }}\right)_{P,T}}$.

Естественно, необходимы также граничные условия для скорости потока, магнитного поля и разности температур, и многое зависит от того, как они ставятся в той или иной модели. Наибольший разброс имеет место в отношении потока тепла и вещества на границах между внутренним и внешним ядром, а также между внешним ядром и мантией, причём существенную роль играет неоднородность мантии и процессов в ней из-за тектоники плит^[17][18][29], которые, что немаловажно, протекают на порядки медленнее, нежели в ядре, что значительно осложняет комплексный анализ задачи.

Удобнее решать эту систему уравнений в безразмерном виде, вводя характерные величины длины, времени, скорости, магнитного поля и т. д.; тогда в них будут входить следующие безразмерные параметры^[17][18][30]:

Параметр	Формула	Определение	Значение в ядре Земли	Примечание
Входные параметры
Число Рэлея	${\displaystyle Ra={\frac {g_{0}\alpha \beta _{0}R_{0}^{3}}{\nu \kappa }}}$, где β0 — градиент температур на границе внешнего ядра (при r=R0). В зависимости от модели, встречаются и другие определения: ${\displaystyle {\frac {g_{0}\alpha \beta _{0}D}{\Omega \kappa }}}$ (D — толщина внешнего ядра), ${\displaystyle {\frac {g_{0}\alpha Q_{0}}{2k\kappa \Omega }}}$ (${\displaystyle Q_{0}=4\pi R_{0}^{2}\kappa \beta _{0}}$ — полный тепловой поток), ${\displaystyle {\frac {g_{0}\alpha \beta _{1}R_{0}^{2}}{\eta \Omega }}}$ (β1 — градиент температур на границе внутреннего и внешнего ядра) и т. п.[17]	соотношение интенсивности плавучести и вязкости, определяющее величину энергии, доступной системе для осуществления конвекции: конвекционный механизм теплопереноса будет преобладать над теплопроводностью, при Ra, большем некоторого критического значения	1024-1030, в зависимости от определения[17][24]
Число Экмана	${\displaystyle E={\frac {\nu }{2\Omega R_{0}^{2}}}}$	соотношение вязкости (внутреннего трения) и силы Кориолиса: меньшее значение соответствует более быстрому вращению, и наоборот	10−15
Число Прандтля, а также (при учёте массопереноса) массовое число Прандтля	${\displaystyle Pr={\frac {\nu }{\kappa }}}$, ${\displaystyle Pc={\frac {\nu }{\kappa _{\xi }}}}$	соотношение характерных времён диффузии вязкой и тепловой, то есть кинематической вязкости и температуропроводности	~10−1	предположительно при преобладании турбулентной диффузии все числа Прандтля стремятся к 1, хотя вопрос о турбулентности в ядре изучен ещё недостаточно
Магнитное число Прандтля	${\displaystyle Pm={\frac {\nu }{\eta }}}$	соотношение характерных времён диффузии магнитной и вязкой, то есть магнитных сил к силам внутреннего трения	10−6
Число Тейлора	${\displaystyle Ta=\left({\frac {2\Omega R_{0}^{2}}{\nu }}\right)^{2}={\frac {1}{E^{2}}}}$	соотношение между силой Кориолиса и силами вязкого трения
Модифицированное число Рэлея	${\displaystyle Ra_{M}={\frac {\alpha \beta _{0}g_{0}R_{0}^{2}}{2\Omega \kappa }}=E\cdot Ra}$	соотношение между силой Архимеда и силой Кориолиса
Магнитное число Экмана	${\displaystyle E_{M}={\frac {\eta }{2\Omega R_{0}^{2}}}={\frac {E}{Pm}}}$	соотношение периода вращения и характерного времени магнитного взаимодействия
Соотношение коэффициентов диффузии магнитной и тепловой	${\displaystyle q={\frac {\kappa }{\eta }}={\frac {Pm}{Pr}}}$		1,7⋅10-5[24], 2⋅10-7[17]
Вычисляемые величины
Магнитное число Рейнольдса	${\displaystyle Rm={\frac {u_{0}R_{0}}{\eta }}}$, где u0 — характерная скорость потока. Локально в каждой точке величина определяется как ${\displaystyle Rm={\frac {|\mathbf {u} \times \mathbf {B} |}{|\eta \mathbf {\nabla } \times \mathbf {B} |}}}$	отношение характерного кинетического времени к коэффициенту магнитной диффузии, то есть магнитной индукции и диффузии	102-103[17][24][30]	Динамо возможно лишь при достижении порогового значения Rm, то есть при условии, что интенсивность роста энергии магнитного поля за счёт работы динамо против силы Лоренца −u•(J × B) превосходит по величине μ0ηJ2, интенсивность диссипации магнитной энергии в тепло, — это соответствует Rm>1, но этого далеко не достаточно: величина -u•(J × B) не должна быть всегда отрицательной[17]. Иногда вводятся также магнитные числа Рейнольдса для альфа-эффекта ${\displaystyle Rm_{\alpha }={\frac {\alpha R_{0}}{\eta }}}$ и омега-эффекта ${\displaystyle Rm_{\omega }={\frac {\omega R_{0}^{2}}{\eta }}}$, для характеристики вкладов этих механизмов[24].
Число Элсассера	${\displaystyle \Lambda ={\frac {B_{0}^{2}}{2\Omega \eta \mu _{0}\rho _{0}}}}$, где B0 — характерная величина магнитного поля,	соотношение между силой Лоренца и силой Кориолиса	${\displaystyle O}$(10)	равно 1 для магнитного поля, равного 1 в безразмерных единицах
Число Россби	${\displaystyle Ro={\frac {u_{0}}{\Omega R_{0}}}}$	соотношение силы инерции и силы Кориолиса	10−6

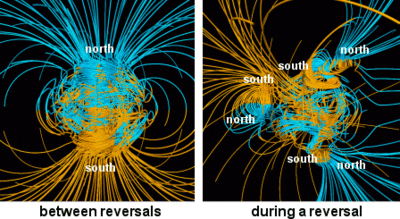
Эту систему дифференциальных уравнений в частных производных ввиду её сложности можно точно решить только численно, и такая возможность технически появилась лишь относительно недавно. Задача численного моделирования — выяснить, описывает ли решение наблюдаемую динамику геомагнитного поля^[17]. Получаемое в результате решения магнитное поле должно быть способно возбуждать токи, порождающие магнитное поле далее, и т. д. Сложность состоит в недостаточности информации о внутреннем ядре, в частности, об источниках тепла, вызывающих конвекцию^[23]. Большие трудности вызывает описание мелкомасштабных структур и расчёт характеристик для них, например, Слой Экмана толщиной 10 см (пусть даже 10 м) на поверхности ядра радиусом 3500 км^[17]. Исключительная малость безразмерных параметров E и Pm и, наоборот, большое значение Rm до сих пор являются недостижимыми при численном моделировании^[18].

Прорыв в этом отношении был достигнут в 1995 году в работах групп из Японии^[32] и Соединённых Штатов^[31][33]. Начиная с этого момента, результаты ряда работ численного моделирования удовлетворительно воспроизводят качественные характеристики геомагнитного поля в динамике, в том числе инверсии^[16][34]. Эталонной моделью считается совокупный результат работы шести научных групп в конце 90-х гг.^[35], где ключевые безразмерные параметры полагались равными Ra=10⁵, E=10⁻³, Pr=1, Pm=5, что очень далеко от реальных значений, но принципиально, что в рамках неё тем не менее существует стабильное решение, и она широко используется для оценки точности других методов^[18].

Вместо точного численного решения, однако, можно построить систему обыкновенных дифференциальных уравнений низкого порядка, грубо отражающую основные особенности оригинальной нелинейной задачи, чтобы приближённо смоделировать поведение системы с точки зрения теории динамических систем^[16][30]. Также аналитически можно оценить поведение системы в асимптотическом пределе^[18][21]. Это позволяет моделировать различные режимы динамо, анализировать связь между параметрами^[24].

Экспериментальное изучение динамо-эффекта также сопряжено с огромными сложностями, так как в лабораторных условиях, естественно, крайне затруднительно воспроизвести условия, создаваемые внутри Земли либо других астрономических объектов — звёзд и планет. Основной проблемой является малость магнитного числа Прандтля, характеризующего экспериментально доступные жидкости^[18][26]. Поэтому с середины XX века осуществлено лишь три успешных реализации гидромагнитного динамо научными группами в Риге^[36][37], Карлcруэ^[38] и Кадараше^[39][40], причём строго говоря, ни один из них нельзя считать прямым аналогом природного процесса^[26]. Сейчас наиболее крупные исследования ведутся в Мэрилендском университете с использованием жидкого натрия и в Висконсинском университете, где необходимые для генерации динамо условия моделируются на горячей плазме^[41].

Проблемой современного геомагнетизма является так называемый Новый парадокс ядра^[42] В рамках традиционной теории динамо для генерации самоподдерживающегося магнитного поля необходимо твёрдое внутреннее ядро. Однако в начале 2010-х гг исследования показали, что твёрдое ядро могло образоваться всего около 1,5 миллиардов лет назад^[43][44], тогда как магнитное поле существовало уже 3,4 миллиарда лет назад^[45], а по некоторым данным даже 4,2 млрд лет назад^[46], то есть вскоре после формирования самой планеты. Следовательно, либо твёрдое ядро всё-таки сформировалось гораздо раньше^[47][48], либо на ранних этапах динамо реализовывалось по какому-то иному механизму^[49][50], например, некоторые ученые полагают^[51], что объяснением парадоксу может служить большая теплоотдача ядра и меньшая — мантии (в таком случае конвекция тепла возможна ещё до образования твердого ядра), однако даже изменённые значения теплопроводности не объясняют парадокс полностью. Разрабатываются также гипотезы о том, что магнитное поле Земли на ранних этапах её существования обеспечивается кристаллизацией минерального вещества — диоксида кремния^[52] либо оксида магния^[53]. На 2017 г. вопрос о возрасте твёрдого ядра и магнитном поле в ранние геологические периоды остаётся открытым^[34].

Исследования остаточной намагниченности, приобретённой изверженными горными породами при остывании их ниже точки Кюри, свидетельствуют о неоднократных инверсиях магнитного поля Земли, зафиксированных в полосовых магнитных аномалиях океанической коры, параллельных осям срединных океанических хребтов. В океанической коре, таким образом, записаны все изменения магнитного поля Земли за последние 240 млн лет. Сопоставляя участки с одинаковой намагниченностью по разные стороны океанических хребтов, можно определить, когда эти участки начали расходиться.

Впервые координаты магнитного полюса в Северном полушарии были определены в 1831 году, повторно — в 1904 году, затем в 1948 году и 1962, 1973, 1984, 1994 годах; в Южном полушарии — в 1841 году, повторно — в 1908 году^[54]. Смещение магнитных полюсов регистрируется с 1885 года. За последние 100 лет магнитный полюс в Южном полушарии переместился^[55] почти на 900 км и вышел в Южный океан^[56]. Новейшие данные^[57] по состоянию арктического магнитного полюса (движущегося по направлению к Восточно-Сибирской мировой магнитной аномалии через Северный Ледовитый океан) показали, что с 1973 по 1984 год его пробег составил 120 км, с 1984 по 1994 год — более 150 км. Хотя эти данные расчётные, они подтверждены замерами северного магнитного полюса.

После 1831 года, когда положение полюса было зафиксировано впервые, к 2019 году полюс сместился уже более чем на 2300 км в сторону Сибири и продолжает двигаться с ускорением. Скорость его перемещения увеличилась с 15 км в год в 2000 году до 55 км в год в 2019 году. Такой быстрый дрейф приводит к необходимости более частой корректировки навигационных систем, использующих магнитное поле Земли, например, в компасах в смартфонах или в резервных системах навигации кораблей и самолётов^[58].

Напряжённость земного магнитного поля падает, причём неравномерно. За последние 22 года она уменьшилась в среднем на 1,7 %, а в некоторых регионах, — например в южной части Атлантического океана, — на 10 %. В некоторых местах напряжённость магнитного поля, вопреки общей тенденции, даже возросла.

Ускорение движения полюсов (в среднем на 3 км/год²) и движение их по коридорам инверсии магнитных полюсов (эти коридоры позволили выявить более 400 палеоинверсий) позволяет предположить, что в данном перемещении полюсов следует усматривать не экскурс, а очередную инверсию магнитного поля Земли^[59].

В физике космических лучей широко используются специфические координаты в геомагнитном поле, названные в честь учёного Карла Мак-Илвейна (Carl McIlwain), первым предложившего их использование^[60], так как они основаны на инвариантах движения частиц в магнитном поле. Точка в дипольном поле характеризуется двумя координатами (L, B), где L — так называемая магнитная оболочка, или параметр Мак-Илвейна (англ. L-shell, L-value, McIlwain L-parameter), B — магнитная индукция поля (обычно в Гс). За параметр магнитной оболочки обычно принимается величина L, равная отношению среднего удаления реальной магнитной оболочки от центра Земли в плоскости геомагнитного экватора, к радиусу Земли.^[61]

Ещё несколько тысячелетий назад в Древнем Китае было известно, что намагниченные предметы располагаются в определённом направлении, в частности стрелка компаса всегда занимает определённое положение в пространстве. Благодаря этому человечество с давних пор получило возможность при помощи такой стрелки (компаса) ориентироваться в открытом море вдали от берегов. Однако до плавания Колумба из Европы в Америку (1492 г.) особого внимания к исследованию такого явления никто не проявлял, так как ученые того времени полагали, что оно происходит в результате притяжения стрелки Полярной звездой. В Европе и омывающих её морях компас в то время устанавливался почти по географическому меридиану. При пересечении же Атлантического океана Колумб заметил, что примерно на полпути между Европой и Америкой стрелка компаса отклонилась почти на 12° к западу. Этот факт сразу же породил сомнение в правильности прежней гипотезы о притяжении стрелки Полярной звездой, дал толчок к серьёзному изучению вновь открытого явления: сведения о магнитном поле Земли были нужны мореплавателям. С этого момента и получила свое начало наука о земном магнетизме, начались повсеместные измерения магнитного склонения, то есть угла между географическим меридианом и осью магнитной стрелки, то есть магнитным меридианом. В 1544 году немецкий учёный Георг Хартман открыл новое явление: магнитная стрелка не только отклоняется от географического меридиана, но, будучи подвешена за центр тяжести, стремится встать под некоторым углом к горизонтальной плоскости, названным магнитным наклонением^[5].

С этого момента наряду с изучением явления отклонения учёные начали также исследовать и наклонение магнитной стрелки. У Хосе де Акосты (одного из основателей геофизики, по словам Гумбольдта) в его Истории (1590) впервые появилась теория о четырёх линиях без магнитного склонения. Он описал использование компаса, угол отклонения, различия между Магнитным и Северным полюсом, а также колебание отклонений от одной точки до другой, идентифицировал места с нулевым отклонением, например, на Азорских островах^[62].

В результате наблюдений было установлено, что как склонение, так и наклонение имеют различные значения в разных точках земной поверхности. При этом их изменения от точки к точке подчиняются некоторой сложной закономерности. Её исследование позволило придворному врачу английской королевы Елизаветы и натурфилософу Уильяму Гильберту выдвинуть в 1600 году в своей книге «О магните» («De Magnete») гипотезу о том, что Земля представляет собой магнит, полюсы которого совпадают с географическими полюсами. Другими словами, У. Гильберт полагал, что поле Земли подобно полю намагниченной сферы. Своё утверждение У. Гильберт основывал на опыте с моделью нашей планеты, представляющей собой намагниченный железный шар, и маленькой железной стрелкой. Главным аргументом в пользу своей гипотезы Гильберт считал, что магнитное наклонение, измеренное на такой модели, оказалось почти одинаковым с наклонением, наблюдавшимся на земной поверхности. Несоответствие же земного склонения со склонением на модели Гильберт объяснял отклоняющим действием материков на магнитную стрелку. Хотя многие факты, установленные позднее, не совпадали с гипотезой Гильберта, она не теряет своего значения и до сих пор. Основная мысль Гильберта о том, что причину земного магнетизма следует искать внутри Земли, оказалась правильной, равно как и то, что в первом приближении Земля действительно является большим магнитом, представляющим собой однородно намагниченный шар^[5].

В 1634 году английский астроном Генри Геллибранд установил, что магнитное склонение в Лондоне меняется со временем. Это стало первым зафиксированным свидетельством вековых вариаций — регулярных (от года к году) изменений средних годовых значений компонентов геомагнитного поля^[5][62].

М. В. Ломоносов в 1759 году в докладе «Рассуждение о большой точности морского пути» дал ценные советы, позволяющие увеличить точность показаний компаса. Для изучения земного магнетизма он рекомендовал организовать сеть постоянных пунктов (обсерваторий), в которых производить систематические магнитные наблюдения; такие наблюдения необходимо широко проводить и на море. Мысль Ломоносова об организации магнитных обсерваторий была осуществлена лишь спустя 60 лет в России^[62].

Углы склонения и наклонения определяют направление в пространстве напряженности магнитного поля Земли, но не могут дать её численного значения. До конца XVIII в. измерения величины напряженности не производились по той причине, что не были известны законы взаимодействия между магнитным полем и намагниченными телами. Лишь после того, как в 1785—1789 гг. французским физиком Шарлем Кулоном был установлен закон, названный его именем, появилась возможность таких измерений. С конца XVIII в., наряду с наблюдением склонения и наклонения, начались повсеместные наблюдения горизонтальной составляющей, представляющей собой проекцию вектора напряженности магнитного поля на горизонтальную плоскость (зная же склонение и наклонение, можно рассчитать и величину полного вектора напряженности магнитного поля)^[5].

Первая теоретическая работа о том, что представляет собой магнитное поле Земли, то есть каковы величина и направление его напряженности в каждой точке земной поверхности, принадлежит немецкому математику Карлу Гауссу. В 1834 г. он дал математическое выражение для составляющих напряженности как функции координат — широты и долготы места наблюдения. Пользуясь этим выражением, можно для каждой точки земной поверхности найти значения любой из составляющих, которые носят названия элементов земного магнетизма. Эта и другие работы Гаусса стали фундаментом, на котором построено здание современной науки о земном магнетизме^[5]. В частности, в 1839 году он доказал, что основная часть магнитного поля выходит из Земли, а причину небольших, коротких отклонений его значений необходимо искать во внешней среде^[62].

В 1831 году английским полярным исследователем Джоном Россом в Канадском архипелаге был открыт северный магнитный полюс — область, где магнитная стрелка занимает вертикальное положение, то есть наклонение равно 90°. А в 1841 г. Джеймс Росс (племянник Джона Росса) достиг другого магнитного полюса Земли, находящегося в Антарктиде^[62].

• Магнитосфера
• Магнитная аномалия
• Полосовые магнитные аномалии
• Ряд Гаусса
• Геофизика
• Intermagnet
• Магнитное поле планет
• Магнитное поле Луны
• Международное геомагнитное аналитическое поле
• Геомагнитная активность

• Петров В. Магнитное поле Земли: история, эволюция и прогнозы (рус.) // Наука и жизнь. — 2021. — № 8. — С. 74—89.
• Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — М.: Наука, 1976.
• Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..
• Короновский Н. В. Магнитное поле геологического прошлого Земли. // Соросовский образовательный журнал, № 5, 1996, с. 56—63
• Ионосфера и плазмосфера / И. А. Кринберг, А. В. Тащилин; СО АН СССР, Сиб. ин-т земного магнетизма, ионосферы и распространения радиоволн ; отв. ред. П. А. Щепкин. - Москва : Наука, 1984. - 189 с.

• Общая интенсивность
• Склонение
• Наклонение
• Горизонтальная интенсивность
• Вертикальная интенсивность

• Инверсии магнитного поля в геологической истории Земли
• Влияние инверсии магнитного поля на климат и эволюцию жизни на Земле.
• Броунов П. И. Магнитные наблюдения // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Текущая информация о состоянии магнитного поля Земли на территории Украины
• Российские ученые перевернули представление о строении Земли