Машина Тьюринга

Маши́на Тью́ринга (сокр. МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для определения понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
То есть всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга[1].
Машина Тьюринга была придумана для доказательства несуществования алгоритма решения тех или иных задач. Однако развитие вычислительной техники стимулировало развитие такого направления, как теория сложности алгоритмов, а машина Тьюринга оказалась очень удобным математическим аппаратом, позволяющим получать оценки как времени выполнения алгоритмов (в частности, и на реальных компьютерах), так и размера памяти, требуемой для вычислений[2].
Устройство
В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки[3][4], и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, оставаться в неподвижном положении, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
Описание машины Тьюринга
Конкретная машина Тьюринга задаётся перечислением букв алфавита A, множеством состояний Q и набором правил перехода, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <qi, aj> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое, машина останавливается. Кроме того, необходимо указать начальное и конечное состояния, начальную конфигурацию на ленте и расположение головки машины.
Пример
Пример машины Тьюринга для умножения чисел в унарной системе счисления. Запись правила перехода «qiaj→qi1aj1R/L/N» следует понимать так: qi — состояние, при котором выполняется это правило, aj — данные в ячейке, в которой находится головка, qi1 — состояние, в которое нужно перейти, aj1 — что нужно записать в ячейку, R/L/N — команда на перемещение.
Машина работает по следующему набору правил:
| q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | q01→q01R | q11→q2aR | q21→q21L | q31 → q4aR | q41→q41R | q71→q2aR | |||
| × | q0×→q1×R | q2×→q3×L | q4×→q4×R | q6×→q7×R | q8×→q9×N | ||||
| = | q2=→q2=L | q4=→q4=R | q7=→q8=L | ||||||
| a | q2a→q2aL | q3a→q3aL | q4a→q4aR | q6a→q61R | q7a→q7aR | q8a→q81L | |||
| * | q0*→q0*R | q3*→q6*R | q4*→q51R | ||||||
| q5 →q2*L |
Описание состояний:
| Начало | |
| q0 | начальное состояние. Ищем «x» справа. При нахождении переходим в состояние q1 |
|---|---|
| q1 | заменяем «1» на «а» и переходим в состояние q2 |
| Переносим все «1» из первого числа в результат | |
| q2 | ищем «х» слева. При нахождении переходим в состояние q3 |
| q3 | ищем «1» слева, заменяем её на «а» и переходим в состояние q4. В случае, если «1» закончились, находим «*» и переходим в состояние q6 |
| q4 | переходим в конец (ищем «*» справа), заменяем «*» на «1» и переходим в состояние q5 |
| q5 | добавляем «*» в конец и переходим в состояние q2 |
| Обрабатываем каждый разряд второго числа | |
| q6 | ищем «х» справа и переходим в состояние q7. Пока ищем, заменяем «а» на «1» |
| q7 | ищем «1» или «=» справа, при нахождении «1» заменяем его на «а» и переходим в состояние q2 при нахождении «=» переходим в состояние q8 |
| Конец | |
| q8 | ищем «х» слева. При нахождении переходим в состояние q9. Пока ищем, заменяем «а» на «1» |
| q9 | терминальное состояние (остановка алгоритма) |
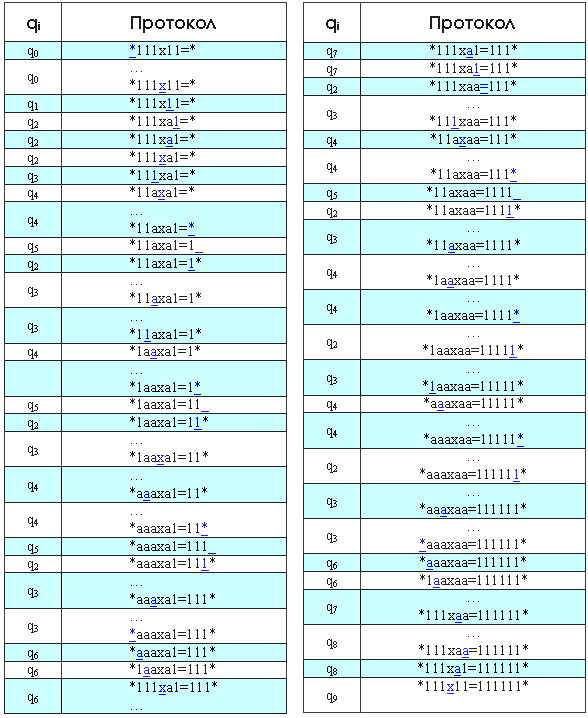
Умножим с помощью МТ 3 на 2 в единичной системе. В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчёркнутый символ).
Начало. Находимся в состоянии q0, ввели в машину данные: *111x11=*, головка машины располагается на первом символе *.
1-й шаг. Смотрим по таблице правил, что будет делать машина, находясь в состоянии q0 и над символом «*». Это правило из 1-го столбца 5-й строки — q0*→q0*R. Это значит, что мы переходим в состояние q0 (то есть не меняем его), символ станет «*» (то есть не изменится) и смещаемся по введённому нами тексту «*111x11=*» вправо на одну позицию (R), то есть на 1-й символ 1. В свою очередь, состояние q01 (1-й столбец 1-я строка) обрабатывается правилом q01→q01R. То есть снова происходит просто переход вправо на 1 позицию. Так происходит, пока мы не станем на символ «х». И так далее: берём состояние (индекс при q), берём символ, на котором стоим (подчёркнутый символ), соединяем их и смотрим обработку полученной комбинации по таблице правил.
Простыми словами, алгоритм умножения следующий: помечаем 1-ю единицу 2-го множителя, заменяя её на букву «а», и переносим весь 1-й множитель за знак равенства. Перенос производится путём поочерёдной замены единиц 1-го множителя на «а» и дописывания такого же количества единиц в конце строки (слева от крайнего правого «*»). Затем меняем все «а» до знака умножения «х» обратно на единицы. И цикл повторяется. Действительно, ведь A умножить на В можно представить как А+А+А В раз. Помечаем теперь 2-ю единицу 2-го множителя буквой «а» и снова переносим единицы. Когда до знака «=» не окажется единиц — значит, умножение завершено.
Полнота по Тьюрингу
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам перехода преобразует входные данные с помощью последовательности элементарных действий.
Элементарность действий заключается в том, что действие меняет лишь небольшой фрагмент данных в памяти (в случае машины Тьюринга — лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга, на ней можно вычислить всё, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.
Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, — это имитация первой машины на второй.
Имитация заключается в следующем. На вход второй машине подаётся описание программы (правил работы) первой машины и входные данные , которые должны были поступить на вход первой машины. Нужно описать такую программу (правила работы второй машины), чтобы в результате вычислений на выходе оказалось то же самое, что вернула бы первая машина, если бы получила на вход данные .
Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать машину Поста, нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью: суммарная память компьютера — оперативная память, жёсткие диски, различные внешние носители данных, регистры и кэш процессора и др. — может быть очень большой, но тем не менее всегда конечна. Теоретический предел количества информации, которая может находиться внутри заданной поверхности, с точностью до множителя равен энтропии чёрной дыры с той же площадью поверхности.
Варианты машины Тьюринга
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Машина Тьюринга, работающая на полубесконечной ленте
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте (то есть на ленте, бесконечной в одну сторону).
Рассмотрим доказательство, приведённое Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых, произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:

Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:
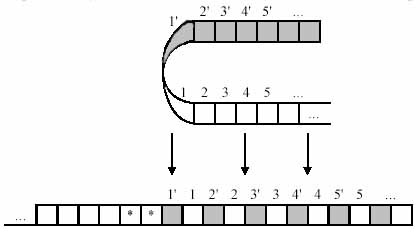
Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:

Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
Двумерные машины Тьюринга
См. также
- JFLAP кроссплатформенная программа — симулятор автоматов, машины Тьюринга, грамматик, рисует граф автомата
- Универсальная машина Тьюринга
- Недетерминированная машина Тьюринга
- Вероятностная машина Тьюринга
- Квантовая машина Тьюринга
- Теория алгоритмов
- Тьюринговская трясина
- Диаграмма Тьюринга
- Машина Минского
Другие абстрактные исполнители и формальные системы вычислений
- Нормальный алгоритм Маркова (продукционное программирование)
- Машина Поста (автоматное программирование)
- Рекурсивная функция (теория вычислимости)
- Лямбда-исчисление (функциональное программирование)
- Brainfuck (императивное программирование)
Примечания
- ↑ Нефёдов, 1992, с. 97.
- ↑ Машины Тьюринга. Дата обращения: 14 октября 2023. Архивировано 5 января 2024 года.
- ↑ Нефёдов, 1992, с. 94.
- ↑ Эббинхауз, 1972, с. 24.
Литература
- Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман. Глава 8. Введение в теорию машин Тьюринга // Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: Вильямс, 2002. — 528 с. — ISBN 0-201-44124-1.
- Карпов Ю. Г. Теория автоматов. — Питер, 2003. — ISBN 5-318-00537-3.
- Эббинхауз Г. Д., Якобс К., Ман Ф. К., Хермес Г. Машины Тьюринга и рекурсивные функции. — М.: Мир, 1972. — 262 с.
- Нефёдов В. Н., Осипова В. А. Курс дискретной математики. — М.: МАИ, 1992. — 260 с.
Ссылки
- Машина Тьюринга // Лекция Александра Шеня в проекте ПостНаука (06.04.2013)





