Медианный граф

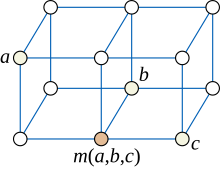
В теории графов медианным графом называется неориентированный граф, в котором любые три вершины a, b, и c имеют единственную медиану — вершину m(a,b,c), которая принадлежит кратчайшим путям между каждой парой вершин a, b и c.

Концепция медианных графов изучалась с давних пор, например, Биргофом и Киссом (Birkhoff, Kiss 1947) или (более явно) Аванном (Avann 1961), но первая статья с именем «Медианные графы» появилась в 1971 (Nebesk'y 1971). Как пишут Чанг^[англ.], Грэм и Сакс (Saks), «медианные графы возникают естественным образом при изучении упорядоченных множеств и дискретных дистрибутивных решёток и имеют обширную литературу».^[1] В филогенетике граф Бунемана, представляющий все максимально правдоподобные^[англ.] эволюционные деревья, является медианным графом.^[2] Медианные графы также появляются в теории социального выбора^[англ.] — если множество возможностей имеет структуру медианного графа, можно среди них определить недвусмысленно предпочтение большинства.^[3]

Обозрение медианных графов можно найти в книгах Klavžar, Mulder, 1999, Bandelt, Chepoi, 2008 и Knuth, 2008.

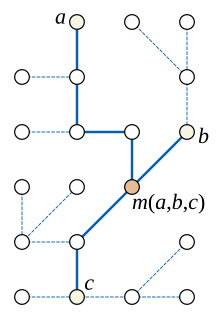
Любое дерево является медианным графом.^[4] В дереве объединение трёх кратчайших путей между парами трёх вершин a, b и c либо само по себе путь, либо поддерево, образованное тремя путями, идущими из одной центральной вершины, имеющей степень три. Если объединение трёх путей является само по себе путём, медиана m(a,b,c) равна одной из вершин a, b или c, в зависимости от того, какая вершина окажется между двумя другими на пути. Если дерево, образованное объединением путей, не является путём, медианой будет центральная вершина поддерева.

Другим примером медианных графов являются решётки. В графе-решётке координаты медианы m(a,b,c) можно найти как медиану координат вершин a, b и c. И наоборот, оказывается, что можно расположить вершины на целочисленной решётке так, что медианы можно вычислить как медианы координат .^[5]

Рамочные графы^[6], планарные графы, в которых все внутренние грани являются четырёхугольниками и все внутренние вершины имеют четыре и более инцидентных ребра, — это ещё один подкласс медианных графов.^[7] Полимино — это специальный случай рамочных графов, а потому тоже образует медианный граф.

Симплекс-граф^[англ.] κ(G) произвольного неориентированного графа G имеет вершину для каждой клики (полный подграф) графа G, и две вершины соединены ребром, если соответствующие клики отличаются только одной вершиной. Медиану заданных трёх клик можно образовать при помощи мажоритарного правила, позволяющего определить, какие вершины клик включать. Симплекс-граф — это медианный граф, в котором это правило определяет медиану каждой тройки вершин.

Никакой цикл длины, отличной от четырёх, не может быть медианным графом, поскольку любой такой цикл имеет три вершины a, b и c, которые соединены тремя кратчайшими путями, не имеющими пересечений.

В произвольном графе для любых двух вершин a и b минимальное число рёбер между ними называется расстоянием, которое обозначается как d(x,y). Интервал вершин, лежащих на кратчайшем пути между a и b, определяется как

I(a,b) = {v | d(a,b) = d(a, v) + d(v, b)}.

Медианный граф определяется как граф, для любых трёх вершин a, b и c которого эти интервалы пересекаются в одной точке:

Для всех a, b и c |I(a,b) ∩ I(a,c) ∩ I(b,c)| = 1.

Таким же образом, для любых трёх вершин a, b и c можно найти вершину m(a,b,c), такую, что невзвешенное расстояния в графе удовлетворяют равенствам

• d(a,b) = d(a,m(a,b,c)) + d(m(a,b,c),b)
• d(a,c) = d(a,m(a,b,c)) + d(m(a,b,c),c)
• d(b,c) = d(b,m(a,b,c)) + d(m(a,b,c),c)

и m(a,b,c) является единственной вершиной, для которой это верно.

Можно также определить медианные графы как решения задач 2-выполнимости, как редукцию гиперкубов, как графы конечных медианных алгебр, как графы Бунемана систем разбиения Хэлли, и как графы с виндексом (windex) 2. Смотрите разделы ниже.

В теории решёток граф конечной решётки имеет вершину для каждого элемента решётки и ребро для каждой пары элементов отношения покрытия^[англ.] решётки. Решётки обычно представляются визуально как диаграммы Хассе, которые являются рисунками графов решёток. Эти графы, особенно для дистрибутивных решёток, оказываются тесно связанными с медианными графами.

В дистрибутивной решётке Биркхофа самодвойственная тернарная операция медианы^[8]

m(a,b,c) = (a ∧ b) ∨ (a ∧ c) ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) ∧ (b ∨ c),

удовлетворяет некоторым ключевым аксиомам, которые свойственны обычным медианам чисел в отрезке от 0 до 1 и медианным алгебрам^[англ.]:

• Идемпотентность: m(a, a, b) = a для всех a и b.
• Коммутативность: m(a,b,c) = m(a, c, b) = m(b, a, c) = m(b, c, a) = m(c, a, b) = m(c, b, a) для всех a, b, и c.
• Дистрибутивность: m(a, m(b, c, d), e) = m(m(a, b, e), c, m(a, d, e)) для всех a, b, c, d, и e.
• Нейтральные элементы: m(0,a,1) = a для всех a.

Дистрибутивный закон можно заменить ассоциативным:^[9]

• Ассоциативность: m(x,w,m(y,w,z)) = m(m(x,w,y),w,z)

Операцию медианы можно использовать так же для определения понятия интервалов для распределённых решёток:

I(a,b) = {x | m(a, x, b) = x} = {x | a ∧ b ≤ x ≤ a ∨ b}.^[10]

Граф конечной дистрибутивной решётки имеет ребро между вершинами a и b, когда I(a,b) = {a,b}. Для любых двух вершин a и b этого графа интервал I(a,b), определённый в терминах теории решёток, состоит из вершин кратчайшего пути из a в b, и это совпадает с интервалами из теории графов, определённых ранее. Для любых трёх элементов решётки a, b и c, m(a,b,c) — это единственное пересечение трёх интервалов I(a,b), I(a,c) и I(b,c).^[11] Таким образом, граф произвольной конечной распределённой решётки является медианным графом. И наоборот, если медианный граф G содержит две вершины 0 и 1, такие, что любые другие вершины лежат на кратчайшем пути между этими двумя (эквивалентно, m(0,a,1) = a для всех a), то мы можем определить распределённую решётку, в которой a ∧ b = m(a,0,b) и a ∨ b = m(a,1,b), и G будет графом этой решётки.^[12]

Дуффус и Райвел (Duffus, Rival 1983) описывают графы дистрибутивных решёток как сохраняющие диаметр редукции гиперкубов. Обобщённо — любой медианный граф порождает тернарную операцию m, удовлетворяющую законам идемпотентности, коммутативности и дистрибутивности, но, возможно, без единичного элемента распределённой решётки. Любая тернарная операция на конечном множестве, удовлетворяющая этим трём свойствам (но не обязательно имеющая элементы 0 и 1) порождает медианный граф.^[13]

Говорят, что в медианном графе множество вершин S является выпуклым, если для любых двух вершин a и b, принадлежащих S, весь интервал I(a,b) является подмножеством S. Эквивалентно, согласно двум определениям интервалов выше, S является выпуклым, если оно содержит любой кратчайший путь между двумя вершинами, или оно содержит медиану любых трёх точек, две из которых лежат в S. Заметим, что пересечение любой пары выпуклых множеств само выпукло.^[14]

Выпуклые множества в медианном графе имеют свойство Хэлли^[англ.]: если F является произвольным семейством попарно пересекающихся выпуклых множеств, то все множества F имеют общую точку.^[15] Так, пусть F имеет только три выпуклых множества S, T и U. Пусть a — пересечения пары S и T, b — пересечения пары T и U, а c — пересечения пары S и U. Тогда любой кратчайший путь из a в b должен лежать внутри T ввиду выпуклости, и, таким же образом, любой кратчайший путь между любыми двумя парами вершин должен лежать внутри двух других множеств, но m(a,b,c) принадлежит путям между всеми тремя парами вершинами, так что оно лежит внутри всех трёх множеств. Если F содержит более чем три выпуклых множества, результат получаем по индукции по числу множеств, — можно заменить любую пару множеств в F их пересечением, что оставляет полученные множества попарно пересекающимися.

Особенно важным семейством выпуклых множеств в медианном графе, играющем роль, подобную полупространствам в евклидовом пространстве, являются множества

W_uv = {w | d(w,u) < d(w,v)},

которые определены для каждого ребра uv графа. Простыми словами, W_uv состоит из вершин, которые ближе к u, чем к v, или, что эквивалентно, из вершин w, для которых кратчайший путь из v в w проходит через u. Чтобы показать, что W_uv выпукло, предположим, что w₁w₂…w_k — произвольный кратчайший путь, начинающийся и кончающийся внутри W_uv. Тогда w₂ должен также лежать внутри W_uv, в противном случае две точки m₁ = m(u,w₁,w_k) и m₂ = m(m₁,w₂…w_k) будут двумя различными медианами u, w₁, и w_k, что противоречит определению медианного графа, в котором медиана единственна по определению. Таким образом, каждая вершина на кратчайшем пути между двумя вершинами W_uv также лежит в W_uv, так что W_uv содержит все кратчайшие пути между вершинами, что является одним из определений выпуклости.

Свойство Хэлли для множеств W_uv играет ключевую роль в описании медианных графов как задачи 2-выполнимости.

Медианные графы имеют тесную связь с множествами решений задач 2-выполнимости^[англ.], которые можно использовать для описания этих графов и с помощью которых можно показать связь с отображением гиперкубов, сохраняющих смежность.^[16]

Экземпляр 2-выполнимости состоит из набора булевских переменных и коллекции утверждений, ограничений^[англ.] на некоторых парах переменных, чтобы избежать некоторых комбинаций значений. Обычно такие задачи выражаются в конъюнктивной нормальной форме, в которой каждое утверждение выражается дизъюнкцией, а всё множество ограничений выражается конъюнкцией утверждений, например,

${\displaystyle (x_{11}\lor x_{12})\land (x_{21}\lor x_{22})\land \cdots \land (x_{n1}\lor x_{n2})\land \cdots .}$

Решением такого экземпляра является назначение значений «истина»^[англ.] переменным, чтобы удовлетворить все утверждения, или, что эквивалентно, что утверждения конъюнктивной нормальной формы дают значения «истина» при подстановке значений. Семейство всех решений имеет естественную структуру медианной алгебры, где медиана трёх решений образуется выбором мажоритарного значения трёх значений. Легко проверить напрямую, что это медианное значение не может нарушать утверждения. Таким образом, эти решения образуют медианный граф, в котором соседи каждого решения образуются путём отрицания множества переменных, для всех из которых все значения внутри множеств либо равны, либо не равны.

И наоборот, любой медианный граф G можно представить в виде множества решений экземпляра задачи 2-выполнимости. Чтобы найти такое представление, создадим экземпляр задачи 2-выполнимости, в которой каждая переменная описывает направление одного из рёбер графа (назначение направления ребру приводит к ориентированным графам) и каждое ограничение включает две ориентированные дуги, только если существует вершина v, для которой обе дуги лежат на кратчайшем пути из других вершин в вершину v. Каждая вершина v графа G соответствует решению экземпляра задачи 2-выполнимости, в котором все дуги направлены в v. Каждое решение экземпляра должно получаться из некоторой вершины v этим способом, где v — общее пересечение множеств W_uw для дуг, направленных из w к u. Это общее пересечение существует ввиду свойства Хэлли множеств W_uw. Таким образом, решения экземпляра этой задачи 2-выполнимости соответствуют один к одному вершинам графа G.

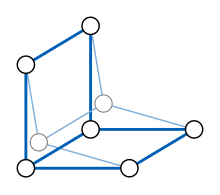
Редукция графа G — это отображение графа G в один из его подграфов с сохранением смежности.^[17] Точнее, это гомоморфизм φ из G в себя, в котором φ(v) = v для каждой вершины v в подграфе φ(G). Образ редукции называется редукцией графа G. Редукции — это примеры коротких отображений: расстояние между φ(v) и φ(w) для любых v и w не больше расстояния между v и w, и эти расстояния равны, если обе вершины v и w принадлежат φ(G). Таким образом, редукция должна быть изометрическим подграфом графа G: расстояния в редукции равны соответствующим расстояниям в G.

Если G является медианным графом, а a, b и c — три произвольные вершины редукции φ(G), то вершина φ(m(a,b,c)) должна быть медианой a, b и c, а следовательно, должна быть равна m(a,b,c). Таким образом, φ(G) содержит медианы всех троек вершин и должен быть медианным графом. Другими словами, семейство медианных графов замкнуто по отношению операции редукции.^[18]

Граф гиперкуба, в котором вершины соответствуют всем возможным k-битным векторам и в котором две вершины связны, если соответствующие вектора отличаются единственным битом, является специальным случаем k-мерного графа решётки, а потому медианным графом. Медиану трёх битовых векторов a, b и c можно вычислить, взяв мажоритарное значение битов a, b и c. Поскольку медианные графы замкнуты по отношению к операции редукции и включают гиперкубы, любая редукция гиперкуба является медианным графом.

И наоборот, любой медианный граф должен быть редукцией гиперкуба.^[19] Это можно видеть из описанной выше связи между медианными графами и задачей 2-выполнимости. Пусть G представляет решения экземпляра задачи 2-выполнимости. Без потери общности этот экземпляр можно сформулировать так, что никакие две переменные всегда равны или не равны во всех решениях. Тогда пространство всех назначений значений переменным образуют гиперкуб. Для любого утверждения, образованного дизъюнкцией двух переменных или их отрицаний, в экземпляре задачи 2-выполнимости, можно образовать редукцию гиперкуба, в которой назначение переменных, нарушающее это утверждение, отображается в назначение переменных, в которых обе переменные удовлетворяют утверждению, но не меняют другие переменные. Композиция редукций, построенных таким образом для каждого утверждения, даёт редукцию гиперкуба в пространство решений экземпляра задачи, а потому даёт представление графа G как редукцию гиперкуба. В частности, медианные графы изометричны подграфам гиперкубов, а потому являются частичным кубом. Однако не все частичные кубы являются медианными графами. Например, цикл с шестью вершинами является частичным кубом, но не медианным графом.

Имрих и Клавжар (Imrich, Klavžar 1998) пишут, что изометричное вложение медианного графа в гиперкуб можно построить за время O(m log n), где n и m — число вершин и рёбер графа.^[20]

Задачи проверки, является ли граф медианным, и содержит ли граф треугольники, обе хорошо изучены, и как отмечают Имрих, Клавжар и Мулдер (Imrich, Klavžar, Mulder 1999), в некотором смысле они вычислительно эквивалентны.^[21] Таким образом, лучшее известное время для проверки, есть ли в графе треугольники, равное O(m^1.41),^[22] можно использовать как оценку времени проверки, является ли граф медианным, и любое продвижение в задаче распознавания медианных графов приведёт к продвижению в алгоритмах определения треугольников в графах.

Для доказательства эквивалентности в одном направлении, предположим, что задан граф G и нужно проверить, есть ли в нём треугольники. Создадим из G другой граф H, имеющий в качестве вершин множества из нуля, одной или двух смежных вершин графа G. Два таких множества смежны в H, если они отличаются только одной вершиной. Как альтернативное описание H можно образовать путём разбиения каждого ребра G на два и добавления новой вершины, соединённой со всеми вершинами исходного графа G. Этот граф H является частичным кубом по построению, но он будет медианным, только когда G не содержит треугольников — если a, b и c образуют треугольник в G, то {a,b}, {a,c} и {b,c} не имеют медиан в H, поскольку такая медиана должна была бы соответствовать множеству {a,b,c}, но множества из трёх и более вершин G не образуют вершин в H. Таким образом, G не содержит треугольников тогда и только тогда, кода H является медианным графом. В случае, когда G не содержит треугольников, H является его симплекс-графом^[англ.]. Алгоритм эффективной проверки, является ли H медианным графом, по этому построению может быть использован для проверки отсутствия треугольников в графе G. Такое преобразование сохраняет вычислительную сложность задачи, поскольку размер H пропорционален размеру G.

Сведение в другом направлении, от поиска треугольников к проверке, является ли граф медианным, более сложно и зависит от описанного алгоритма распознавания медианного графа (Hagauer, Imrich, Klavžar 1999), который проверяет некоторые необходимые условия медианного графа в почти линейное время. Новый ключевой шаг использует поиск в ширину для разложения графа на уровни согласно их расстоянию от произвольно выбранного корня, образуя тем самым граф, в котором две вершины смежны, если у них есть общий сосед на предыдущем уровне, и поиск треугольников происходит в этих графах. Медиана любого такого треугольника должна быть общим соседом трёх вершин треугольника. Если такой сосед не существует, граф не является медианным. Если все треугольники найдены и у всех них есть медианы, а также предыдущий алгоритм определяет, что граф удовлетворяет остальным условиям медианных графов, то он должен быть медианным. Заметим, что этот алгоритм требует не только проверки отсутствия треугольников, но и перечисление треугольников в графе уровней. В произвольном графе перечисление треугольников требует иногда время Ω(m^3/2), поскольку некоторые графы имеют столько треугольников. Однако Хагауэр (Hagauer и др.) показал, что число треугольников, возникающих в уровневых графах, почти линейно, что позволило Алону (Alon и др.) использовать технику быстрого умножения матриц для поиска треугольников.

Филогенетика — это вывод филогенетических деревьев из наблюдаемых характеристик биологического вида. Такие деревья должны располагать виды в различных вершинах и могут содержать дополнительные скрытые вершины, но скрытые вершины должны иметь три и более инцидентных рёбер и должны быть помечены характеристиками. Характеристики являются бинарными, если они имеют только два возможных значения, и множество видов и их характеристик показывает совершенную историю развития^[англ.], если существует эволюционное дерево, в котором вершины (виды и скрытые вершины), помеченные любыми определёнными характеристиками, образуют непрерывное поддерево. Если дерево с совершенной историей развития невозможно, часто желательно найти максимально правдоподобное^[англ.] дерево, или, что эквивалентно, минимизировать число случаев, когда конечные точки рёбер дерева имеют различные характеристики, суммируя по всем рёбрам и по всем характеристикам.

Бунеман (Buneman 1971) описал метод вывода совершенных эволюционных деревьев для бинарных характеристик, если они существуют. Его метод обобщается естественным образом для построения медианного графа любого множества видов и бинарных характеристик, и этот граф называют медианной сетью или графом Бунемана^[23] и он представляет собой филогенетическую сеть^[англ.]. Любое эволюционное дерево максимального правдоподобия можно вложить в граф Бунемана, в том смысле, что рёбра дерева идут по путям в графе и число изменений характеризующих значений на ребре дерева равно числу соответствующих путей. Граф Бунемана будет деревом в том и только в том случае, когда совершенная история развития существует. Это происходит, когда не существует двух несовместимых характеристик, для которых наблюдаются все четыре комбинации значений.

Чтобы сформировать граф Бунемана для множества видов и характеристик, сначала избавляемся от избыточных видов, которые неотличимы от некоторых других видов и от избыточных характеристик, которые всегда совпадают с некоторыми другими характеристиками. Затем образуем скрытую вершину для любой комбинации значений характеристик, таких, что любые два значения существуют в известных видах. В показанном примере есть малые бесхвостые коричневые мыши, малые серебристые бесхвостые мыши, малые коричневые хвостатые мыши, большие хвостатые коричневые мыши и большие серебристые хвостатые мыши. Метод построения графа Бунемана создаст скрытую вершину, соответствующую неизвестному виду малых серебристых хвостатых мышей, поскольку любая попарная комбинация (малая и серебристая, малая и хвостатая и серебристая и хвостатая) появляются в некоторых других видах. Однако метод не предполагает существование больших коричневых бесхвостых мышей, поскольку нет вида больших и, одновременно, бесхвостых мышей. После того, как скрытые вершины определены, образуем рёбра между каждой парой видов или скрытых вершин, которые отличаются одной характеристикой.

Можно эквивалентным образом описать набор бинарных характеристик как систему разбиений, семейств множеств^[англ.]* со свойством, что дополнение любого множества в семействе принадлежит семейству. Эта система разбиений представляет множество для каждого значения характеристик, состоящее из видов, которые имеют это значение. Если включить скрытые вершины, результирующая система разбиений имеет свойство Хэлли^[англ.] — любые попарные пересечения подсемейств не пусты. В некотором смысле медианные графы можно представить как производные от систем разбиений Хэлли — пары (W_uv, W_vu), определённые для каждого ребра uv медианного графа, образуют систему разбиений Хэлли, так, что в случае применения построения графа Бунемана к этой системе скрытые вершины не понадобятся, и результатом будет исходный граф.^[24]

В статьях Bandelt, Forster, Sykes, Richards, 1995 и Bandelt, Macaulay, Richards, 2000 описывается техника упрощения ручного вычисления графов Бунемана и показано использование этой конструкции для визуального представления генетических связей людей.

• Прямое произведение любых двух медианных графов является тоже медианным графом. Медианы в результирующем графе можно найти путём независимого поиска медиан обоих сомножителей, точно так же, как медианы графов решёток можно найти путём независимого поиска медиан по всем линейным измерениям.

• виндекс графа измеряет число поисков вперёд^[англ.], необходимых для оптимального решения задачи, в которой задана последовательность вершин графа s_i и следует найти другую последовательность вершин t_i, минимизирующую сумму расстояний d(s_i,t_i) и d(t_{i − 1},t_i). Медианные графы — это в точности те графы, для которых windex равен 2. В медианном графе, оптимальный выбор — это множество t_i = m(t_{i − 1},s_i,s_{i + 1}).^[1]

• Свойство иметь единственную медиану называется также свойство единственности точек Штайнера.^[1] Оптимальное дерево Штайнера для трёх вершин a, b и c в медианном графе можно найти как объединение трёх кратчайших путей, из a, b и c в m(a,b,c). Бандельт и Бартелеми (Bandelt, Barthélémy 1984) изучали задачу нахождения вершины, минимизирующей сумму расстояний^[англ.] до каждой вершины заданного множества, и показали, что она имеет единственное решение для любого нечётного числа вершин медианного графа. Они также показали, что эта медиана вершин множества S медианного графа удовлетворяет критерию Кондорсе^[англ.] победителя выборов: по сравнению с другими вершинами он ближе всех к большинству вершин S.

• Как и в случае частичных кубов, любой медианный граф с n вершинами имеет максимум (n/2) log₂ n рёбер. Однако число рёбер не может быть слишком маленьким: Клавжар, Мулдер и Шкрековски (Klavžar, Mulder, Škrekovski 1998) доказали, что в любом медианном графе выполняется неравенство 2n − m − k ≤ 2, где m — число рёбер и k — размерность гиперкуба, из которого граф получен. Это неравенство превращается в равенство тогда и только тогда, когда медианный граф не содержит кубов. Всё это следствия другого равенства для медианных графов: эйлерова характеристика Σ (-1)^dim(Q) всегда равна единице, где сумма берётся по всем гиперкубам подграфов Q данного медианного графа.^[25]

• Только регулярные медианные графы являются гиперкубами.^[26]

• Median graphs, Information System for Graph Class Inclusions.
• Network, Free Phylogenetic Network Software. Network generates evolutionary trees and networks from genetic, linguistic, and other data.
• PhyloMurka, open-source software for median network computations from biological data.