
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе. Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму.
В квантовой механике задача о части́це в одноме́рном периоди́ческом потенциа́ле — идеализированная задача, которая может быть решена аналитически, без упрощений. При решении предполагается, что функция потенциала задана на всем бесконечном пространстве и периодична, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, где всегда существует как минимум один дефект — поверхность кристалла.
Краевая задача — задача о нахождении решения заданного дифференциального уравнения, удовлетворяющего краевым (граничным) условиям в концах интервала или на границе области. Краевые задачи для гиперболических и параболических уравнений часто называют начально-краевыми или смешанными, потому что в них задаются не только граничные, но и начальные условия.
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних, находятся все переменные системы.
Ме́тод моме́нтов — метод оценки неизвестных параметров распределений в математической статистике и эконометрике, основанный на предполагаемых свойствах моментов. Идея метода заключается в замене истинных соотношений выборочными аналогами.
Теория Калуцы — Клейна — одна из многомерных теорий гравитации, позволяющая объединить два фундаментальных физических взаимодействия: гравитацию и электромагнетизм. Теория была впервые опубликована в 1921 году немецким математиком Теодором Калуцей, который расширил пространство Минковского до 5-мерного пространства и получил из уравнений своей теории уравнения общей теории относительности и классические уравнения Максвелла. Обоснование ненаблюдаемости пятого измерения было предложено шведским физиком Оскаром Клейном в 1926 году.
Физи́ческая кине́тика — микроскопическая теория процессов в неравновесных средах. В кинетике методами квантовой или классической статистической физики изучают процессы переноса энергии, импульса, заряда и вещества в различных физических системах и влияние на них внешних полей. В отличие от термодинамики неравновесных процессов и электродинамики сплошных сред, кинетика исходит из представления о молекулярном строении рассматриваемых сред, что позволяет вычислить из первых принципов кинетические коэффициенты, диэлектрические и магнитные проницаемости и другие характеристики сплошных сред. Физическая кинетика включает в себя кинетическую теорию газов из нейтральных атомов или молекул, статистическую теорию неравновесных процессов в плазме, теорию явлений переноса в твёрдых телах и жидкостях, кинетику магнитных процессов и теорию кинетических явлений, связанных с прохождением быстрых частиц через вещество. К ней же относятся теория процессов переноса в квантовых жидкостях и сверхпроводниках и кинетика фазовых переходов.

Треуго́льник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью.
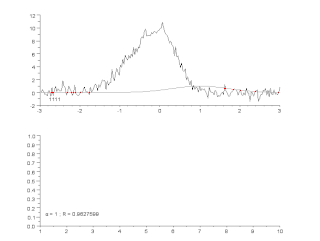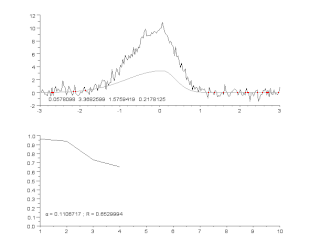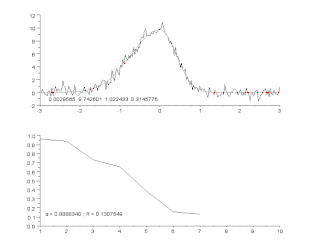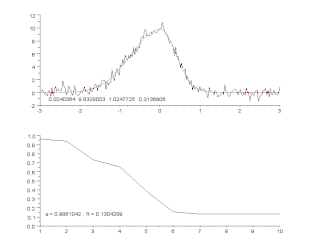
Алгоритм Гаусса — Ньютона используется для решения задач нелинейным методом наименьших квадратов. Алгоритм является модификацией метода Ньютона для нахождения минимума функции. В отличие от метода Ньютона, алгоритм Гаусса — Ньютона может быть использован только для минимизации суммы квадратов, но его преимущество в том, что метод не требует вычисления вторых производных, что может оказаться существенной трудностью.

Теорема Тейлора даёт приближение к функции, дифференцируемой k раз, вблизи данной точки с помощью многочлена Тейлора k-го порядка. Для аналитических функций многочлен Тейлора в данной точке является частичной суммой их ряда Тейлора, который, в свою очередь, полностью определяет функцию в некоторой окрестности точки. Точное содержание теоремы Тейлора до настоящего времени не согласовано. Конечно, существует несколько версий теоремы, применимых в различных ситуациях, и некоторые из этих версий содержат оценки ошибки, возникающей при приближении функции с помощью многочлена Тейлора.
Тороидальная система координат — ортогональная система координат в пространстве, координатными поверхностями которой являются торы, сферы и полуплоскости. Данная система координат может быть получена посредством вращения двумерной биполярной системы координат вокруг оси, равноудалённой от фокусов биполярной системы.
Метод итерации или метод простой итерации — численный метод решения системы линейных алгебраических уравнений. Суть метода заключается в нахождении по приближённому значению величины следующего приближения, являющегося более точным.

Метод сопряженных градиентов — численный метод решения систем линейных алгебраических уравнений, является итерационным методом Крыловского типа.
Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS) — итерационный метод численной оптимизации, предназначенный для нахождения локального максимума/минимума нелинейного функционала без ограничений.
Стабилизированный метод бисопряжённых градиентов — итерационный метод решения СЛАУ крыловского типа. Разработан Ван дэр Ворстом (англ.) для решения систем с несимметричными матрицами. Сходится быстрее, чем обычный метод бисопряженных градиентов, который является неустойчивым, и поэтому применяется чаще.

Бидуга́ — гладкая плоская кривая, составленная из двух круговых дуг, меньших полной окружности. Одной из дуг может быть отрезок прямой. Бидуги были предложены для геометрического моделирования кривых с заданными граничными точками и касательными в них. В классе бидуг эта задача имеет целое семейство решений, и требует дополнительных условий для нахождения конкретных кривых. Таковыми могут быть задание кривизны или поворота одной из дуг, фиксированная длина кривой, требование минимизации скачка кривизны в точке сопряжения, и т. п.
В теории многих тел термин функция Грина иногда используется как синоним корреляционной функции, но относится к корреляторам операторов поля или операторам рождения и уничтожения.
Групповой анализ дифференциальных уравнений — раздел математики, изучающий свойства симметрии дифференциальных уравнений относительно различных преобразований зависимых и независимых переменных. Включает в себя методы и прикладные аспекты дифференциальной геометрии, теории групп и алгебр Ли, вариационного исчисления и является, в свою очередь, эффективным инструментом исследования в теории ОДУ, ДУЧП и математической физике.
Круговой критерий — условие абсолютной устойчивости нелинейной системы управления c нелинейностью, лежащей в секторе.
































