Краевая задача — задача о нахождении решения заданного дифференциального уравнения, удовлетворяющего краевым (граничным) условиям в концах интервала или на границе области. Краевые задачи для гиперболических и параболических уравнений часто называют начально-краевыми или смешанными, потому что в них задаются не только граничные, но и начальные условия.
Со́бственный ве́ктор — понятие в линейной алгебре, определяемое для произвольного линейного оператора как ненулевой вектор, применение к которому оператора даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение. Скаляр, на который умножается собственный вектор под действием оператора, называется собственным числом линейного оператора, соответствующим данному собственному вектору. Одним из представлений линейного оператора является квадратная матрица, поэтому собственные векторы и собственные значения часто определяются в контексте использования таких матриц.
Метод Якоби — разновидность метода простой итерации для решения системы линейных алгебраических уравнений. Назван в честь Карла Густава Якоби.
В этой статье рассматривается математический базис общей теории относительности.
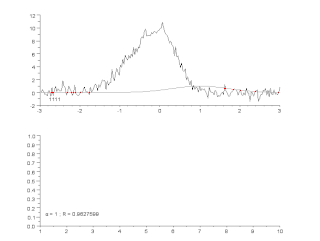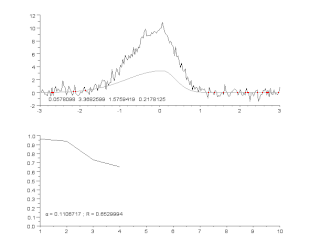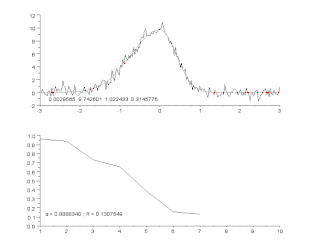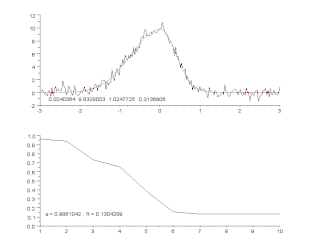
Алгоритм Гаусса — Ньютона используется для решения задач нелинейным методом наименьших квадратов. Алгоритм является модификацией метода Ньютона для нахождения минимума функции. В отличие от метода Ньютона, алгоритм Гаусса — Ньютона может быть использован только для минимизации суммы квадратов, но его преимущество в том, что метод не требует вычисления вторых производных, что может оказаться существенной трудностью.
Фотоупругость, фотоэластический эффект, пьезооптический эффект — возникновение оптической анизотропии в первоначально изотропных твёрдых телах под действием механических напряжений. Открыта Т. И. Зеебеком (1813) и Д. Брюстером (1816). Фотоупругость является следствием зависимости диэлектрической проницаемости вещества от деформации и проявляется в виде двойного лучепреломления и дихроизма, возникающих под действием механических нагрузок. При одноосном растяжении или сжатии изотропное тело приобретает свойства оптически одноосного кристалла с оптической осью, параллельной оси растяжения или сжатия. При более сложных деформациях, например при двустороннем растяжении, образец становится оптически двухосным.
Спектральная теорема — класс теорем о матрицах линейных операторов, дающих условия, при которых такие матрицы могут быть диагонализированы, то есть представлены в виде диагональной матрицы в некотором базисе. Эти теоремы позволяют свести вычисления, включающие диагонализируемые матрицы к гораздо более простым вычислениям, использующим соответствующие диагональные матрицы.
Бетатронные колебания — быстрые поперечные колебания, совершаемые частицей в фокусирующих магнитных полях ускорителя. Бетатронные колебания — основной предмет изучения электронной оптики, раздела физики ускорителей.
Сглаживающий сплайн это метод сглаживания с использованием сплайн-функций.
Молекулярные орбитали — математическая функция, описывающая волновое поведение электронов в молекуле.
Алгоритм вычисления собственных значений — алгоритм, позволяющий определить собственные значения и собственные векторы заданной матрицы. Создание эффективных и устойчивых алгоритмов для этой задачи является одной из ключевых задач вычислительной математики.
Байесовская линейная регрессия — это подход в линейной регрессии, в котором статистический анализ проводится в контексте байесовского вывода: когда регрессионная модель имеет ошибки, имеющие нормальное распределение, и, если принимается определённая форма априорного распределения, доступны явные результаты для апостериорных распределений вероятностей параметров модели.
Степенной метод, или метод степенных итераций, — итерационный алгоритм поиска собственного значения с максимальной абсолютной величиной и одного из соответствующих собственных векторов для произвольной матрицы.
Обратный степенной метод или метод обратных итераций — итеративный алгоритм вычисления собственных векторов и значений. Позволяет искать собственные вектора и собственные значения произвольной матрицы. Обычно используется для вычисления собственных векторов, если для собственных значений известны достаточно хорошие приближения.
Нелинейная задача собственных значений — это обобщение обычной задачи собственных значений до уравнений, зависящих от собственных значений нелинейно. В частности, эта задача относится к уравнениям вида
Обобщённый собственный вектор 
матрицы 
— вектор, который удовлетворяет определённым критериям, которые слабее, чем критерии для (обычных) собственных векторов.
Численные методы линейной алгебры — это методы приближенного решения задач из области вычислительной математики и линейной алгебры. Целью дисциплины является разработка и анализ алгоритмов для численного решения матричных задач. Наиболее важными задачами являются решение систем линейных алгебраических уравнений и вычисление собственных значений.
