
Нейро́нная сеть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети У. Маккалока и У. Питтса. После разработки алгоритмов обучения получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
Многосеточный метод — метод решения системы линейных алгебраических уравнений, основанный на использовании последовательности уменьшающихся сеток и операторов перехода от одной сетки к другой. Сетки строятся на основе больших значений в матрице системы, что позволяет использовать этот метод при решении эллиптических уравнений даже на нерегулярных сетках.
Метод обратного распространения ошибки — метод вычисления градиента, который используется при обновлении весов многослойного перцептрона. Впервые метод был описан в 1974 году Александром Галушкиным, а также независимо и одновременно Полом Вербосом. Далее существенно развит в 1986 году Дэвидом Румельхартом, Джеффри Хинтоном и Рональдом Уильямсом и независимо и одновременно Барцевым и Охониным. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Градиентный спуск, метод градиентного спуска — численный метод нахождения локального минимума или максимума функции с помощью движения вдоль градиента, один из основных численных методов современной оптимизации.

Перцептро́н — математическая или компьютерная модель восприятия информации мозгом, предложенная Фрэнком Розенблаттом в 1957 году и впервые воплощённая в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.
Де́льта-пра́вило — метод обучения перцептрона по принципу градиентного спуска по поверхности ошибки. Дельта-правило развилось из первого и второго правил Хебба. Его дальнейшее развитие привело к созданию метода обратного распространения ошибки.
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида — Соломона, работающие с байтами (октетами).
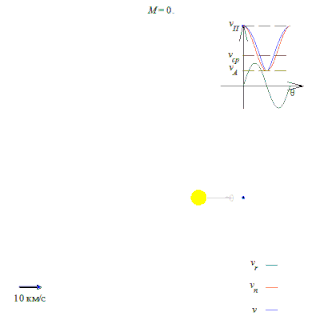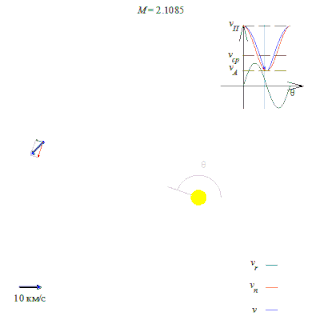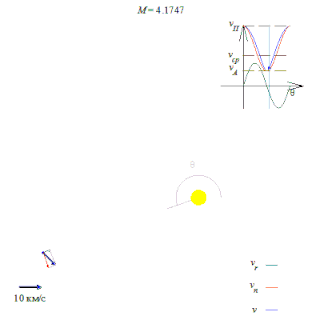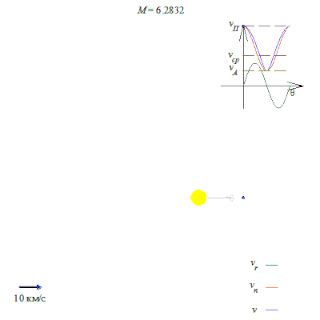
Орбитальная скорость тела — скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.

Многослойный перцептрон — частный случай перцептрона Розенблатта, в котором один алгоритм обратного распространения ошибки обучает все слои. Название по историческим причинам не отражает особенности данного вида перцептрона, то есть не связано с тем, что в нём имеется несколько слоёв. Особенностью является наличие более чем одного обучаемого слоя. Необходимость в большом количестве обучаемых слоёв отпадает, так как теоретически единственного скрытого слоя достаточно, чтобы перекодировать входное представление таким образом, чтобы получить линейную разделимость для выходного представления. Существует предположение, что, используя большее число слоёв, можно уменьшить число элементов в них, то есть суммарное число элементов в слоях будет меньше, чем если использовать один скрытый слой. Это предположение успешно используется в технологиях глубокого обучения и имеет обоснование.
Теорема сходимости перцептрона — это теорема, описанная и доказанная Ф. Розенблаттом. Она показывает, что элементарный перцептрон, обучаемый по методу коррекции ошибки, независимо от начального состояния весовых коэффициентов и последовательности появления стимулов всегда приведёт к достижению решения за конечный промежуток времени. Ф. Розенблаттом также были представлены доказательства ряда сопутствующих теорем, следствия из которых позволяли сделать вывод о том, каким условиям должны соответствовать архитектура искусственных нейронных сетей и методы их обучения.
Метод коррекции ошибки — метод обучения перцептрона, предложенный Фрэнком Розенблаттом. Представляет собой такой метод обучения, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.
Перцептроны с обратной связью — наиболее общий вид перцептронов, некоторые виды которых были описаны Ф. Розенблаттом. Они отличаются от простых перцептронов наличием обратной связи. Благодаря этому слои элементов, находящихся сравнительного далеко от сенсорных входов, могут воздействовать на активность слоёв, расположенных ближе к входу. Согласно современной классификации этот тип нейронной сети относится к рекуррентным нейронным сетям.
Перцептрон с переменными S-A связями — перцептрон Розенблатта с несколькими R-элементами и переменными (обучаемыми) S-A и A-R связями. В названии акцент сделан на S-A связи, так как это последнее снятое Розенблаттом ограничение при рассмотрении элементарного перцептрона, в результате чего получена система самого общего вида с топологической структурой S -> A -> R. Данный перцептрон является эквивалентом многослойного перцептрона Румельхарта, хотя самим Розенблаттом под этим названием был рассмотрен случай только с двумя слоями связей. Но этого достаточно, чтобы охарактеризвать этот подвид перцептронов в том же отношении, что было сделано Румельхартом. Для более сложного анализа возможностей перцептронов Розенблатт переходит к четырёхслойным перцептронам, считая только их многослойными перцептронами.

Перцептрон является одной из первых моделей искусственной нейронной сети. Несмотря на то, что модель предложена Фрэнком Розенблаттом в 1957 году, о её возможностях и ограничениях до сегодняшнего дня не всё известно. В 1969 году Марвин Минский и Сеймур Паперт посвятили критике перцептрона целую книгу, которая показала некоторые принципиальные ограничения одной из разновидности перцептронов.
А́льфа-систе́ма подкрепле́ния — система подкрепления, при которой веса всех активных связей  , которые оканчиваются на некотором элементе
, которые оканчиваются на некотором элементе  , изменяются на одинаковую величину
, изменяются на одинаковую величину  , или с постоянной скоростью в течение всего времени действия подкрепления, причём веса неактивных связей за это время не изменяются. Перцептрон, в котором используется α-система подкрепления, называется α-перцептроном. Подкрепление называется дискретным, если величина изменения веса является фиксированной, и непрерывным, если эта величина может принимать произвольное значение.
, или с постоянной скоростью в течение всего времени действия подкрепления, причём веса неактивных связей за это время не изменяются. Перцептрон, в котором используется α-система подкрепления, называется α-перцептроном. Подкрепление называется дискретным, если величина изменения веса является фиксированной, и непрерывным, если эта величина может принимать произвольное значение.
Позиционная весовая матрица (ПВМ) — биоинформатический метод, который применяется для поиска мотивов в биологических последовательностях.
ПВМ может быть построена на основе множественного выравнивания родственных последовательностей, или последовательностей, выполняющих близкие функции. ПВМ используется во многих современных алгоритмах для обнаружения новых мотивов.
Онлайновое машинное обучение — это метод машинного обучения, в котором данные становятся доступными в последовательном порядке и используются для обновления лучшего предсказания для последующих данных, выполняемого на каждом шаге обучения. Метод противоположен пакетной технике обучения, в которой лучшее предсказание генерируется за один раз, исходя из полного тренировочного набора данных. Онлайновое обучение является общей техникой, используемой в областях машинного обучения, когда невозможна тренировка по всему набору данных, например, когда возникает необходимость в алгоритмах, работающих с внешней памятью. Метод используется также в ситуациях, когда алгоритму приходится динамически приспосабливать новые схемы в данных или когда сами данные образуются как функция от времени, например, при предсказании цен на фондовом рынке. Алгоритмы онлайнового обучения могут быть склонны к катастрофическим помехам, проблеме, которая может быть решена с помощью подхода пошагового обучения.
Анализ независимых компонент, называемый также Метод независимых компонент (МНК) — это вычислительный метод в обработке сигналов для разделения многомерного сигнала на аддитивные подкомпоненты. Этот метод применяется при предположении, что подкомпоненты являются негауссовыми сигналами и что они статистически независимы друг от друга. АНК является специальным случаем слепого разделения сигнала. Типичным примером приложения является задача вечеринки с коктейлем — когда люди на шумной вечеринке выделяют голос собеседника, несмотря на громкую музыку и шум людей в помещении: мозг способен фильтровать звуки и сосредотачиваться на одном источнике в реальном времени.
Тест ассоциативности — проверка бинарной операции на ассоциативность. Наивная процедура проверки, заключающаяся в переборе всех возможных троек аргументов операции, требует  времени, где
времени, где  — размер множества, над которым определена операция. Ранние тесты ассоциативности не давали асимптотических улучшений по сравнению с наивным алгоритмом, однако позволяли улучшить время работы в некоторых частных случаях. Например, Роберт Тарьян в 1972 году обнаружил, что предложенный в 1949 году тест Лайта позволяет выполнить проверку за
— размер множества, над которым определена операция. Ранние тесты ассоциативности не давали асимптотических улучшений по сравнению с наивным алгоритмом, однако позволяли улучшить время работы в некоторых частных случаях. Например, Роберт Тарьян в 1972 году обнаружил, что предложенный в 1949 году тест Лайта позволяет выполнить проверку за  , если исследуемая бинарная операция обратима. Первый вероятностный тест, улучшающий время работы с
, если исследуемая бинарная операция обратима. Первый вероятностный тест, улучшающий время работы с  до
до  , был предложен в 1996 году Шридхаром Раджагопаланом и Леонардом Шульманом. В 2015 году был предложен квантовый алгоритм, проверяющий операцию на ассоциативность за время
, был предложен в 1996 году Шридхаром Раджагопаланом и Леонардом Шульманом. В 2015 году был предложен квантовый алгоритм, проверяющий операцию на ассоциативность за время  , что является улучшением по сравнению с поиском Гровера, работающим за
, что является улучшением по сравнению с поиском Гровера, работающим за  .
.
Подпись при обучении с ошибками в кольце — один из классов криптосистем с открытым ключом, основанный на задаче обучения с ошибками в кольце, который заменяет используемые алгоритмы подписи RSA и ECDSA. В течение последнего десятилетия проводились активные исследования по созданию криптографических алгоритмов, которые остаются безопасными, даже если у злоумышленника есть ресурсы квантового компьютера. Подпись при обучении с ошибками в кольце относится к числу пост-квантовых подписей с наименьшим открытым ключом и размерами подписи. Использование общей проблемы обучения с ошибками в криптографии было введено Одедом Регевым в 2005 году и послужило источником нескольких криптографических разработок. Основоположники криптографии при обучении с ошибками в кольце, считают, что особенностью этих алгоритмов, основанных на обучении с ошибками, является доказуемое сокращение известных сложных задач. Данная подпись имеет доказуемое сокращение до задачи нахождения кратчайшего вектора в области криптографии на решётках. Это означает, что если можно обнаружить атаку на криптосистему RLWE, то целый класс предполагаемых сложных вычислительных проблем будет иметь решение. Первая подпись на основе RLWE была разработана Вадимом Любашевским и уточнена в 2011 году. Данная статья освещает фундаментальные математические основы RLWE и основана на схеме под названием GLYPH.
































