Механизм Липкина — Посселье

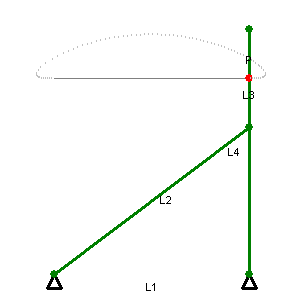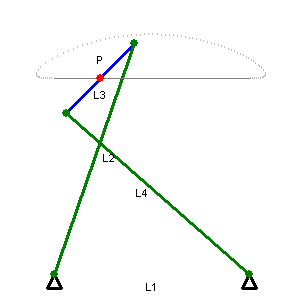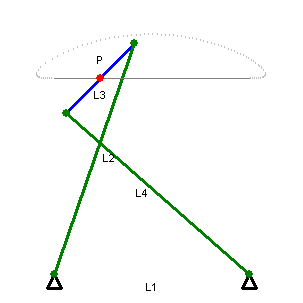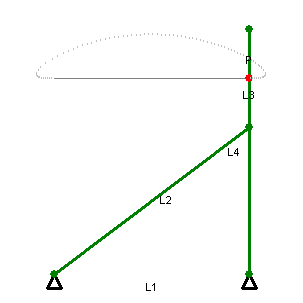
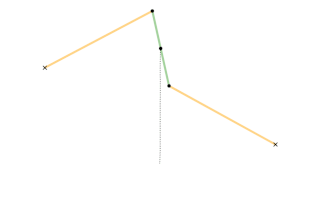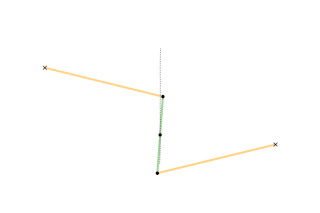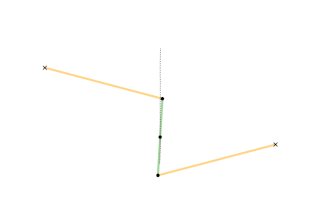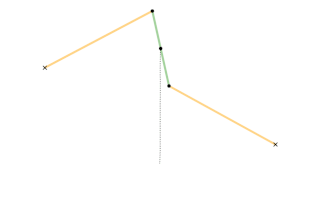
звенья, показанные одним цветом, имеют одинаковую длину
Механизм Липкина — Посселье (или инверсор Липкина — Посселье) — механизм, способный преобразовывать вращательное движение в совершенное прямолинейное, и наоборот.
Изобретён в 1864 году Шарлем Посселье[фр.] и независимо Липманом Израилевичем Липкином в 1871 году.[1][2]. До этого изобретения существовавшие методы создания прямолинейного движения требовали наличия направляющих, что особенно значимо для деталей машин и для технологических процессов. В частности, без использования этого или подобных ему изобретений поршень в поршневом насосе нуждается в прочной заделке в месте крепления к штоку (см. плунжер).
Это изобретение сыграло важную роль в развитии паровых машин.[]
Математическое описание механизма Липкина — Посселье прямо связано с инверсией окружности.
Существует также более ранний механизм прямолинейного движения, история которого недостаточно хорошо известна, — механизм Саррюса. Этот механизм появился на 11 лет раньше механизма Липкина — Посселье. Он состоит из нескольких шарнирно-сочленённых прямоугольных пластин, две из которых остаются параллельными, но могут двигаться друг к другу. Механизм Саррюса принадлежит к классу пространственных механизмов, в отличие от механизма Липкина — Посселье, являющегося плоским механизмом.
Геометрия механизма

На геометрических построениях можно увидеть шесть звеньев постоянной длины: OA, OC, AB, BC, CD, DA. Длина звена OA равна длине OC, и длины звеньев AB, BC, CD, DA равны между собой, образуя ромб. В то же время точка O остаётся неподвижной. Если точка B производит вынужденное движение по окружности (на рисунке показанной красным), проходящей через точку О, то точка D обязательно будет двигаться по прямой линии (показана голубым). С другой стороны, если точка B будет вынужденно двигаться по прямой (не проходящей через О), то точка D будет двигаться по окружности, проходящей через О.

Другие способы преобразования вращательного движения в прямолинейное
- Механизм Чебышёва
- Механизм Хойкена
- Механизм Ватта
- Кривошипно-шатунный механизм
- Механизм планшайба-стержни
- Кулачковый механизм
См. также
Ссылки
Примечания
- ↑ Математическое исследование механизма Посселье—Липкина Архивная копия от 6 сентября 2014 на Wayback Machine (англ)
- ↑ Как начертить прямую линию от Дайаны Таймины Архивная копия от 1 декабря 2011 на Wayback Machine (англ)