При́нцип наиме́ньшего де́йствия Га́мильтона, также просто принцип Гамильтона — способ получения уравнений движения физической системы при помощи поиска стационарного значения специального функционала — действия. Назван в честь Уильяма Гамильтона, использовавшего этот принцип для построения так называемого гамильтонова формализма в классической механике.

Уравнение диффузии представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным.
Уравне́ние Шрёдингера — линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму.
Дифференциа́льная геоме́трия кривы́х — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.
Уравне́ние Бо́льцмана — уравнение, названное по имени Людвига Больцмана, который его впервые рассмотрел, и описывающее статистическое распределение частиц в газе или жидкости. Является одним из самых важных уравнений физической кинетики. Уравнение Больцмана используется для изучения переноса тепла и электрического заряда в жидкостях и газах, и из него выводятся транспортные свойства, такие как электропроводность, эффект Холла, вязкость и теплопроводность. Уравнение применимо для разрежённых систем, где время взаимодействия между частицами мало.
Уравне́ния Гамильто́на в физике и математике — система дифференциальных уравнений:


Лагранжева механика — формулировка классической механики, введённая Луи Лагранжем в 1788 году. В лагранжевой механике траектория объекта получается при помощи отыскания пути, который минимизирует действие — интеграл от функции Лагранжа по времени. Функция Лагранжа для классической механики вводится в виде разности между кинетической энергией и потенциальной энергией.
Гамильто́нова меха́ника является одной из формулировок классической механики. Предложена в 1833 году Уильямом Гамильтоном. Она возникла из лагранжевой механики, другой формулировки классической механики, введённой Лагранжем в 1788 году. Гамильтонова механика может быть сформулирована без привлечения лагранжевой механики с использованием симплектических многообразий и пуассоновых многообразий.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.
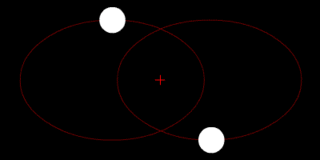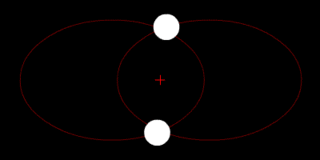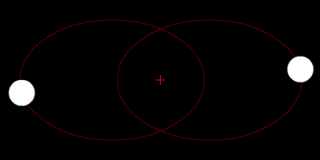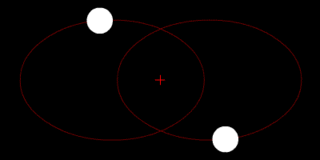
В классической механике, задача двух тел состоит в том, чтобы определить движение двух материальных точек, которые взаимодействуют только друг с другом. Распространённые примеры включают спутник, обращающийся вокруг планеты, планета, обращающаяся вокруг звезды, две звезды, обращающиеся вокруг друг друга, и классический электрон, движущийся вокруг атомного ядра.
Приведённая масса — условная характеристика распределения масс в движущейся механической или смешанной системе, зависящая от физических параметров системы и от её закона движения.
В классической механике уравне́ния Аппе́ля рассматривают как альтернативную формулировку общих уравнений движения, предложенных Ньютоном. Выписаны Полем Аппелем в 1900 . Несмотря на то, что эти уравнения полностью эквивалентны уравнениям, получаемым из законов Ньютона и принципа наименьшего действия, уравнения Аппеля в ряде случаев оказываются более удобными, в частности, в случае, когда система стеснена механическими связями.
Уравне́ния Ра́уса — дифференциальные уравнения движения механической системы с идеальными двусторонними голономными связями.
Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число.
Обобщённые координаты — переменные состояния системы, описывающие конфигурацию динамической системы относительно некоторой эталонной конфигурации в аналитической механике, а конкретно исследовании динамики твёрдых тел в системе многих тел. Эти переменные должны однозначно определять конфигурацию системы относительно эталонной конфигурации. Обобщённые скорости — производные по времени обобщённых координат системы.
В классической механике уравнение Удвадия — Калабы представляет собой метод получения уравнений движения механической системы с ограничениями (связями). Уравнение было впервые получено Фирдаусом Э. Удвадия и Робертом Э. Калабой в 1992 году. Подход основан на принципе наименьшего принуждения Гаусса. Уравнение Удвадия — Калабы применимо к широкому классу связей, как голономных, так и неголономных, если они линейны относительно ускорений. Уравнение также можно обобщить на связи, которые не подчиняются принципу Даламбера.



















