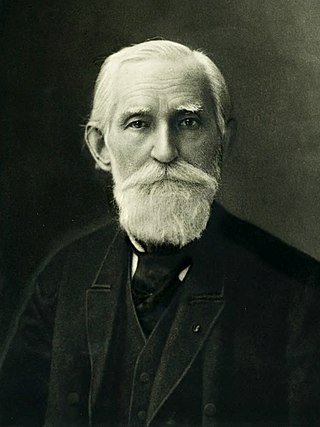Матема́тика — точная формальная наука, первоначально исследовавшая количественные отношения и пространственные формы. В более современном понимании, это наука об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств, — именно тех, которые в качестве аксиом положены в основание той или иной математической теории.
А́лгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики; в этом разделе числа и другие математические объекты обозначаются буквами и другими символами, что позволяет записывать и исследовать их свойства в самом общем виде. Слово «алгебра» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под «алгеброй» понимают раздел математики, посвящённый изучению операций над элементами множеств произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
Теорети́ческая фи́зика — раздел физики, в котором в качестве основного способа познания природы используется создание теоретических моделей явлений и сопоставление их с реальностью. В такой формулировке теоретическая физика является самостоятельным методом изучения природы, хотя её содержание, естественно, формируется с учётом результатов экспериментов и наблюдений за природой.
Аксио́ма, или постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами.
Теория чисел или высшая арифметика — раздел математики, первоначально изучавший свойства целых чисел. В современной теории чисел рассматриваются и другие типы чисел — например, алгебраические и трансцендентные, а также функции различного происхождения, которые связаны с арифметикой целых чисел и их обобщений.
Пафну́тий Льво́вич Чебышёв — русский математик и механик, основоположник петербургской математической школы, академик Петербургской академии наук и ещё 24 академий мира.
Теоре́ма — математическое утверждение, истинность которого устанавливается путём доказательства. Доказательства теорем опираются на ранее доказанные теоремы и общепризнанные утверждения (аксиомы).
Тео́рия игр — математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более стороны, ведущие борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках.
Адрие́н Мари́ Лежа́ндр, фр. Adrien-Marie Legendre — французский математик.
Ива́н Матве́евич Виногра́дов — советский математик, академик АН СССР (1929) по Отделению физико-математических наук (математика).
Конструктивная математика — абстрактная наука о мыслительных конструктивных процессах, человеческой способности осуществлять их, и об их результатах — конструктивных математических объектах. Является результатом развития конструктивного направления в математике — математического мировоззрения, которое в отличие от теоретико-множественного направления считает основной задачей математики исследование конструктивных процессов и конструктивных объектов.
Метаматематика — раздел математической логики, изучающий основания математики, структуру математических доказательств и математических теорий с помощью формальных методов. Термин «метаматематика» буквально означает «за пределами математики».
Арно́ Данжуа́ — французский математик. Основные работы в области гармонического анализа и теории дифференциальных уравнений. Член Парижской Академии наук (1942) и её президент (1962). Иностранный член Академии наук СССР (1971). Награждён золотой медалью имени М. В. Ломоносова АН СССР (1970) «за выдающиеся достижения в области математики».
Ве́кторное исчисле́ние — раздел математики, в котором изучаются свойства операций над векторами.
Джон фон Не́йман — венгеро-американский математик, физик и педагог еврейского происхождения, сделавший важный вклад в квантовую физику, квантовую логику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки.
История теории вероятностей отмечена многими уникальными особенностями. Прежде всего, в отличие от появившихся примерно в то же время других разделов математики, у теории вероятностей по существу не было античных или средневековых предшественников, она целиком — создание Нового времени. Долгое время теория вероятностей считалась чисто опытной наукой и «не совсем математикой», её строгое обоснование было разработано только в 1929 году, то есть даже позже, чем аксиоматика теории множеств (1922). В наши дни теория вероятностей занимает одно из первых мест в прикладных науках по широте своей области применения; «нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы».
Анализ — объединение нескольких разделов математики, исторически выросшее из классического математического анализа и охватывающее, кроме дифференциального и интегрального исчислений, входящих в классическую часть, такие разделы, как теории функций вещественной и комплексной переменной, теории дифференциальных и интегральных уравнений, вариационное исчисление, гармонический анализ, функциональный анализ, теорию динамических систем и эргодическую теорию, глобальный анализ. Нестандартный анализ находится на стыке математической логики и анализа, применяет методы теории моделей для альтернативной формализации, прежде всего, классических разделов.
Владимир Фёдорович Демьянов — советский и российский учёный-математик, доктор физико-математических наук, профессор СПбГУ.
В теории игр, теорема о минимаксе описывает условия, при выполнении которых для функции 
верно, что 
Первой теоремой такого рода стала теорема фон Неймана, доказанная в 1928 году. Именно с её доказательства началось развитие теории игр. Впоследствии её неоднократно обобщали и переформулировали.
