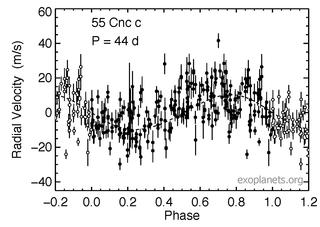
Минимальная масса

Слева: изображение планеты вращающейся вокруг звезды. Всё движение звезды происходит вдоль луча зрения наблюдателя; доплеровская спектроскопия даст истинное значение массы планеты.

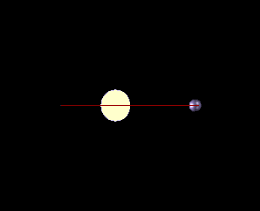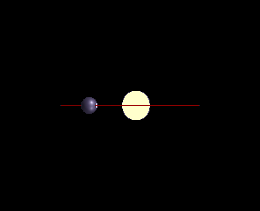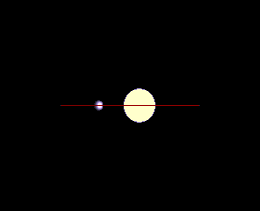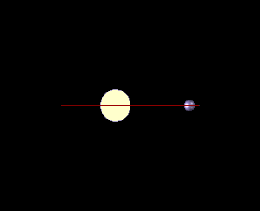
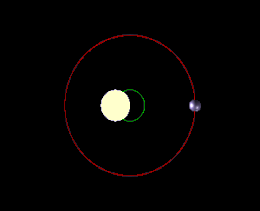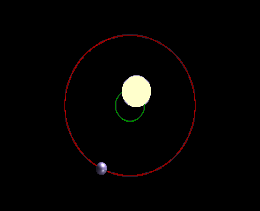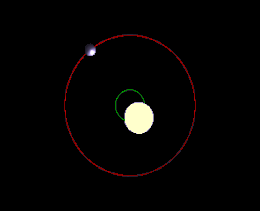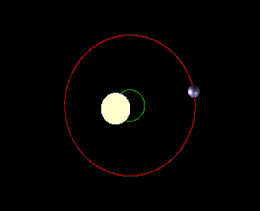
Справа: в этом случае ни одно из движений звезды не происходит вдоль луча зрения наблюдателя, и метод доплеровской спектроскопии вообще не обнаружит планету

В астрономии минимальная масса — это минимальная расчётная масса нижней границы наблюдаемых объектов, таких как планеты, звезды (двойные и кратные системы^[1]), туманности^[2], и черные дыры.

Минимальная масса является широко используемым параметром для внесолнечных планет, определяемых с помощью доплеровской спектроскопии, при которой масса определяется с использованием функции масс двойных звёзд. Этот метод выявляет планеты, измеряя изменения в движении звёзд в зоне прямой видимости, поэтому реальные наклонения орбиты и истинные массы планет обычно неизвестны^[3]. Это результат вычисления функции sin i .

Если можно определить наклон орбиты i, истинная масса может быть получена из рассчитанной минимальной массы с использованием следующего соотношения:

${\displaystyle M_{\text{true}}={\frac {M_{\min }}{\sin i}}\,}$

Вероятно, что наименьшая масса для чёрной дыры приблизительно равна массе Планка (около 2,2⋅10⁻⁸ кг или 22 мкг).

У большинства звёзд планеты не выстроены одну линию по отношению к наблюдателю на Земле, и они не ориентированы так, чтобы они затмевали центр своей звезды и давали зрителю на Земле идеальное покрытие. Именно по этой причине, мы можем только экстраполировать минимальную массу при фиксации колебания звезды, потому что мы не знаем наклона оси планеты и, следовательно, можем рассчитать только ту часть массы, которая колеблет звезду на плоскости небесной сферы.

Для планет вне солнечной системы наклон 0° или 180° соответствует повёрнутой «плашмя» орбите (которая не может наблюдаться методами радиальных скоростей), тогда как наклон 90 ° соответствует орбите видимой с «ребра» (для которой истинная масса равна минимальной массе)^[4].

Планеты с орбитами, сильно наклонёнными к линии обзора с Земли, создают меньшие видимые колебания, и, следовательно, их труднее обнаружить. Одним из преимуществ метода лучевых скоростей является то, что эксцентриситет орбиты планеты может быть измерен напрямую. Одним из основных недостатков метода лучевых скоростей является то, что он может оценить только минимальную массу планеты (${\displaystyle M_{\text{true}}*{\sin i}\,}$)^[5].

Однако, когда в системе имеется несколько планет, которые вращаются относительно близко друг к другу и имеют достаточную массу, анализ орбитальной устойчивости позволяет ограничить максимальную массу этих планет. Метод лучевой скорости может быть использован для подтверждения результатов, полученных методом транзита. Когда оба метода используются в сочетании, тогда может быть оценена истинная масса планеты.

Хотя лучевая скорость звезды даёт только минимальную массу планеты, если спектральные линии планеты можно отличить от спектральных линий звезды, то лучевая скорость самой планеты может быть найдена, и это даёт наклон орбиты планеты. Это позволяет измерять фактическую массу планеты. Это также исключает ложные срабатывания, а также предоставляет данные о составе планеты. Основная проблема заключается в том, что такое обнаружение возможно только в том случае, если планета вращается вокруг относительно яркой звезды и если планета отражает или излучает много света^[6].

Термин «истинная масса» является синонимом термина «масса», но используется в астрономии для дифференциации измеренной массы планеты от минимальной массы, обычно получаемой с помощью методов лучевых скоростей^[7]. Методы, используемые для определения истинной массы планеты, включают измерение расстояния и периода одного из её спутников^[8]. Также для определения массы используются продвинутые методы астрометрии, которые используют движения других планет в той же самой звездной системе^[7], сочетающие методы лучевой скорости с транзитным методом наблюдения (которые указывают на очень малые наклонения орбиты)^[9], и комбинирование методов лучевых скоростей с измерениями звёздного параллакса (которые также определяют наклонения орбиты)^[10].

В тригонометрии единичная окружность — это окружность с радиусом равным единице с центром в начале координат (0,0) в декартовой системе координат.

Пусть линия через начало координат, составляющая угол θ с положительной половиной оси x, пересекает единичную окружность. Координаты x и y этой точки пересечения равны cos(θ) и sin(θ) соответственно. Расстояние точки от начала координат всегда равно 1.

С массой, в 93 раза превышающей массу Юпитера (M_J) или 0,09 массы солнца, AB Золотой Рыбы C, компаньон AB Золотой Рыбы A, является самой маленькой из известных звёзд, у которой существует термоядерный синтез в своём ядре^[11]. Для звёзд металличностью, схожих с Солнцем, теоретическая минимальная масса, которую звезда может иметь и которая все ещё поддерживает синтез в ядре, оценивается примерно в 75 M_J^[12][13]. Однако, когда металличность очень низкая, недавнее исследование самых слабых звёзд обнаружило, что минимальный размер звезды, по-видимому, составляет около 8,3 % от массы Солнца, или около 87 M_J^[13][14]. Меньшие тела называются коричневыми карликами, которые занимают плохо определённую серую область между звёздами и газовыми гигантами.

В принципе, чёрная дыра может иметь любую массу, равную или превышающую массу Планка (около 2,2⋅10⁻⁸ кг или 22 микрограмма)^[15]. Чтобы создать чёрную дыру, нужно сконцентрировать массу или энергию настолько, чтобы вторая космическая скорость для области, в которой она сконцентрирована, превышала скорость света. Это условие даёт радиус Шварцшильда, R = 2GM/c², где G — гравитационная постоянная, c — скорость света, а M — масса чёрной дыры. С другой стороны, комптоновская длина волны λ = h/Mc, где h — постоянная Планка, представляет собой ограничение на минимальный размер области, в которой масса M в состоянии покоя может быть локализована. При достаточно малых М приведённая комптоновская длина волны (λ = ħ/Mc, где ħ — приведенная постоянная Планка) превышает половину радиуса Шварцшильда, и описания чёрной дыры не существует. Таким образом, эта наименьшая масса для чёрной дыры приблизительно равна массе Планка.

Некоторые расширения современной физики предполагают существование дополнительных измерений пространства. В многомерном пространстве-времени сила тяжести увеличивается быстрее с уменьшением расстояния, чем в трёх измерениях. При определённых специальных конфигурациях дополнительных измерений этот эффект может снизить масштаб Планка до диапазона ТэВ. Примеры таких расширений включают большие дополнительные измерения, особые случаи модели Рэндалла – Сундрума^[англ.] и конфигурации теории струн, такие как решения GKP. В таких сценариях, производство чёрной дыры может быть важным и наблюдаемым эффектом на Большом адронном коллайдере (БАК)^{[16][17][18][19][20]}. Это также было бы обычным явлением природы, вызванным космическими лучами.

Все это предполагает, что общая теория относительности остаётся верной на малых расстояниях. Если этого не произойдёт, то другие, в настоящее время неизвестные, эффекты будут ограничивать минимальный размер чёрной дыры. Элементарные частицы имеют квантово-механический, собственный момент импульса (спин). Закон сохранения для общего (орбитального и спинового) углового момента вещества в искривлённом пространстве-времени требует, чтобы пространство-время имело вращение. Самая простая и естественная теория гравитации с вращением — это теория Эйнштейна — Картана^[21][22]. Торсион модифицирует уравнение Дирака в присутствии гравитационного поля, что приводит к пространственному расширению частиц фермионов^[23].

Пространственное расширение фермионов ограничивает минимальную массу чёрной дыры величиной порядка 10¹⁶ кг, показывая, что мини-чёрные дыры не могут существовать. Энергия, необходимая для создания такой чёрной дыры, на 39 порядков больше энергии, доступной на Большом адронном коллайдере, что указывает на то, что БАК не может производить мини-чёрные дыры. Но если возникают чёрные дыры, то общая теория относительности оказывается неверной и не работает на таких малых расстояниях. Правила общей теории относительности будут нарушены, что согласуется с теориями о том, как материя, пространство и время разрушаются вокруг горизонта событий чёрной дыры. Это докажет, что пространственные расширения границ фермионов также будут некорректными. Пределы фермионов предполагают минимальную массу, необходимую для поддержания чёрной дыры, в отличие от минимальной массы, необходимой для образования чёрной дыры, что теоретически достижимо на БАК^[24].