Математи́ческий ана́лиз — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное и интегральное исчисления.
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Формирование дифференциального исчисления связано с именами Исаака Ньютона и Готфрида Лейбница. Именно они чётко сформировали основные положения и указали на взаимно-обратный характер дифференцирования и интегрирования. Создание дифференциального исчисления открыло новую эпоху в развитии математики, положив начало теории рядов, теории дифференциальных уравнений и многому другому. Методы математического анализа нашли применение во всех разделах математики и расширили применение математики в естественных науках и технике.
Ро́тор, рота́ция или вихрь — векторный дифференциальный оператор над векторным полем.
Вариацио́нное исчисле́ние — раздел анализа, в котором изучаются вариации функционалов. Наиболее типичная задача — найти функцию, на которой заданный функционал достигает экстремального значения.
Ко́мпле́ксный ана́лиз, тео́рия фу́нкций ко́мпле́ксного переме́нного — раздел математического анализа, в котором рассматриваются и изучаются функции комплексного аргумента.
Дифференциа́льная геоме́трия кривы́х — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.
Дифференциа́льное уравне́ние в ча́стных произво́дных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.

Точка перегиба — точка плоской кривой, в которой её ориентированная кривизна меняет знак. Если кривая является графиком функции, то в этой точке выпуклая часть функции отделяется от вогнутой.
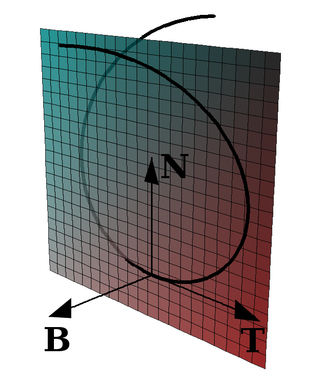
Норма́ль в геометрии — обобщение понятия перпендикуляра к прямой или плоскости на произвольные гладкие кривые и поверхности.
Как и для криволинейных интегралов, существуют два рода поверхностных интегралов.
Теорема разложения Гельмгольца — утверждение о разложении произвольного дифференцируемого векторного поля на две компоненты:
Дифференциальная геометрия поверхностей — исторически важная область дифференциальной геометрии.
Четвёртая проблема Гильберта в списке проблем Гильберта касается базовой системы аксиом геометрии. Проблема состоит в том, чтобы
«Определить все с точностью до изоморфизма реализации систем аксиом классических геометрий, если в них опустить аксиомы конгруэнтности, содержащие понятия угла, и пополнить эти системы аксиомой неравенства треугольника».
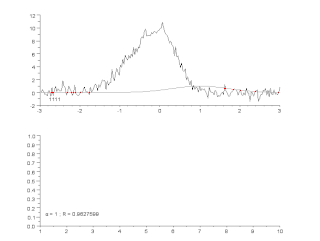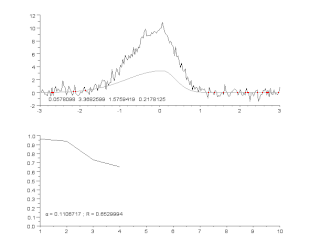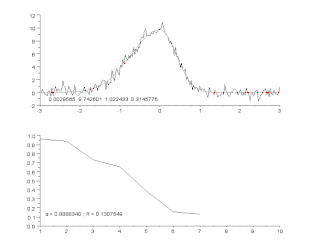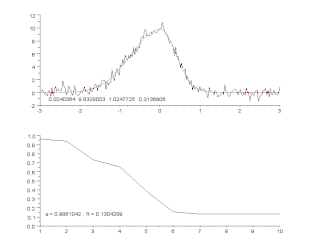
Приближение с помощью кривых — это процесс построения кривой или математической функции, которая наилучшим образом приближается к заданным точкам с возможными ограничениями на кривую. Для построения такого приближения может использоваться либо интерполяция, где требуется точное прохождение кривой через точки, либо сглаживание, когда «сглаживающая» функция проходит через точки приближённо. Связанный раздел — регрессионный анализ, который фокусируется, главным образом, на вопросах статистического вывода, таких как, какая неопределённость заключена в кривой, которая приближает данные с некоторыми случайными ошибками. Построенные кривые могут быть использованы для визуализации данных, для вычисления значений функции в точках, в которых значение не задано и для определения связи между двумя и более переменными. Экстраполяция означает использование полученной кривой за пределами данных, полученных из наблюдения, и порождает некоторую неопределённость, поскольку может зависеть от метода построения кривой.

Поверхность Эннепера — определённый тип самопересекающейся минимальной поверхности.
















