
Коно́ид — линейчатая поверхность, у которой образующие пересекают фиксированную прямую — ось коноида. Если все образующие коноида перпендикулярны его оси, то такой коноид называют прямым.
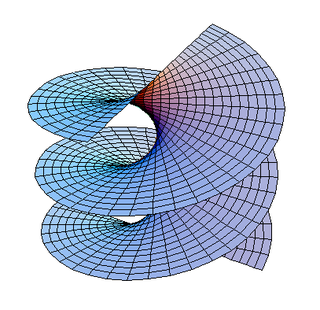
Гелико́ид — винтовая поверхность, описываемая параметрическими соотношениями

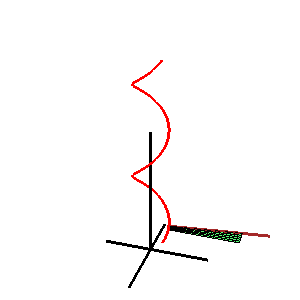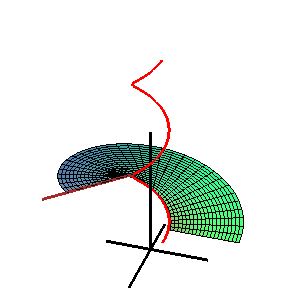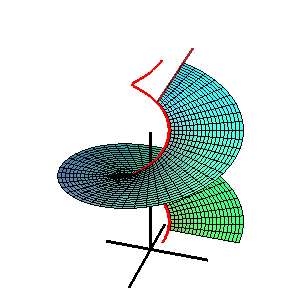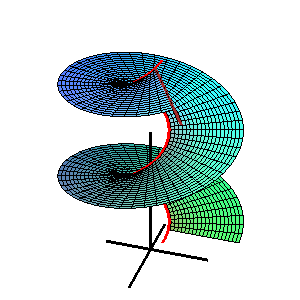
Поверхность Каталана — линейчатая поверхность, прямолинейные образующие которой параллельны одной и той же плоскости. Её стрикционная линия плоская. Радиус-вектор поверхности Каталана:

Уравнение синус-Гордона — это нелинейное гиперболическое уравнение в частных производных в 1 + 1 измерениях, включающее в себя оператор Даламбера и синус неизвестной функции. Изначально оно было рассмотрено в XIX веке в связи с изучением поверхностей постоянной отрицательной кривизны. Это уравнение привлекло много внимания в 1970-х годах из-за наличия у него солитонных решений.
Постоя́нная Катала́на — число, встречающееся в различных приложениях математики — в частности, в комбинаторике. Чаще всего обозначается буквой G, реже — K или C. Она может быть определена как сумма бесконечного знакочередующегося ряда:


Суперквадрики — семейство геометрических поверхностей, определяемых уравнением эллипсоида и других поверхностей второго порядка, где показатели степени 2 заменены произвольным числом. Их можно считать трёхмерными аналогами кривых Ламе (суперэллипсов).

Инверсия кривой — результат применения операции инверсии к заданной кривой C. По отношению к фиксированной окружности с центром O и радиусом k инверсия точки Q — это точка P, лежащая на луче OQ, и OP•OQ = k2. Инверсия кривой C — это множество всех точек P, являющихся инверсиями точек Q, принадлежащих кривой C. Точка O в этом построении называется центром инверсии, окружность называется окружностью инверсии, а k — радиусом инверсии.

Кривая Уатта (лемнискатоида) — плоская алгебраическая кривая шестого порядка, частный случай кривой скольжения. Определяется как геометрическое место точек центров отрезков одинаковой длины, расположенных концами на двух окружностях одинакового радиуса.

Поверхность Дини — пример поверхности постоянной отрицательной кривизны. Она даёт изометрическое погружение области плоскости Лобачевского, ограниченной орициклом.

Поверхность Шерка является примером минимальной поверхности. Шерк описал две полные вложенные минимальные поверхности в 1834 году. Его первая поверхность является дважды периодической поверхностью, а вторая — просто периодической. Они были третьим нетривиальным примером минимальных поверхностей. Две поверхности сопряжены друг другу.

Минимальная поверхность Бура — двухмерная минимальная поверхность, вложенная с самопересечениями в трёхмерное евклидово пространство. Поверхность названа именем Эдмонда Бура, работа которого о минимальных поверхностях получила в 1861 году математический приз Французской академии наук.

Семейство поверхностей Чена — Гакстаттера — это семейство минимальных поверхностей, которое обобщает поверхность Эннепера путём добавления ручек, дающее поверхности ненулевой топологический род.
Минимальные поверхности Шварца — это периодические минимальные поверхности, первоначально описанные Карлом Шварцем.

Трижды периодическая минимальная поверхность — это минимальная поверхность в  , являющаяся инвариантом по переносам в решётке ранга 3.
, являющаяся инвариантом по переносам в решётке ранга 3.
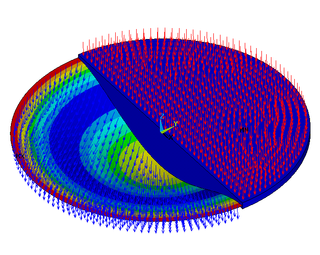
Изгиб пластин в теории упругости относится к расчёту деформаций в пластинах, под действием перпендикулярных к плоскости пластины внешних сил и моментов. Величину отклонения можно определить, решив дифференциальные уравнения соответствующей теории пластин в зависимости от допущений на малость тех или иных параметров. По этим прогибам можно рассчитать напряжения в пластине. При известных напряжениях можно использовать теорию разрушения, чтобы определить, нарушение целостности плиты при данной нагрузке. Деформация пластины является функцией двух координат, поэтому теория пластин формулируется в общем случае в терминах дифференциальных уравнений в двумерном пространстве. Также считается, что пластина изначально имеет плоскую форму.
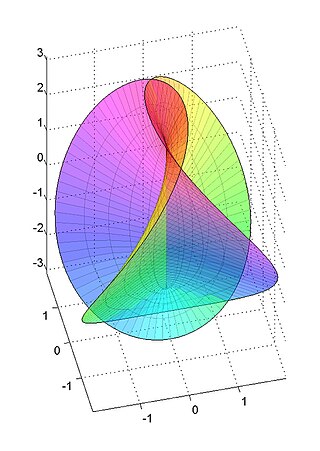
Поверхность Хеннеберга — неориентируемая минимальная поверхность, названная именем немецкого математика Лебрехта Хенненберга.

Минимальная поверхность Римана — однопараметрическое семейство минимальных поверхностей, описанное Бернхардом Риманом в посмертной статье, опубликованной в 1867 году. Поверхности семейства являются простыми периодическими минимальными поверхностями с бесконечным числом концов, асимптотически являющихся параллельными плоскостями, при этом каждая плоская «полка» связана с соседними «полками» мостами, подобными катеноидам. Пересечение этих мостов с горизонтальными плоскостями представляют собой окружности или прямые. Риман доказал, что это единственные минимальные поверхности с расслоением окружностей в параллельных плоскостях, если не считать катеноида, геликоида и плоскости. Эти поверхности также являются единственными нетривиальными минимальными поверхностями в евклидовом трёхмерном пространстве, образованными группой нетривиальных параллельных переносов. Можно добавить дополнительные ручки к поверхности с образованием семейств минимальных поверхностей с увеличенным родом.

Гироид — бесконечно связанная трижды периодическая минимальная поверхность, открытая Аланом Шоэном в 1970 году

Параметризация Вейерштрасса — Эннепера минимальных поверхностей — классический раздел дифференциальной геометрии.


























