Теоре́ма Фа́ри — Ми́лнора утверждает что вариация поворота любого узла превышает  .
.
Дифференциальная геометрия поверхностей — исторически важная область дифференциальной геометрии.

Конфигурация Кремоны — Ричмонда — конфигурация из 15 прямых и 15 точек, по три точки, лежащих на каждой прямой, и через каждую точку проходят 3 прямых, при этом конфигурация не содержит треугольников. Конфигурацию изучали Кремона и Ричмонд. Конфигурация является обобщённым четырёхугольником с параметрами (2,2). Граф Леви конфигурации — это граф Татта — Коксетера.
Плитки Труше — квадратные плитки с рисунком, не обладающим вращательной симметрией. Расположенные в виде квадратной мозаики на плоскости, они могут образовать различные узоры.

Поверхность Боя — первый известный пример погружения вещественной проективной плоскости в трёхмерное евклидово пространство.
Классификация Энриквеса — Кодайры — это классификация компактных комплексных поверхностей на десять классов. Для каждого из этих классов поверхности этих классов можно параметризовать пространством модулей. Для большинства классов пространства модулей хорошо проработаны, но для класса поверхностей общего типа пространства модулей слишком сложны для явного описания, хотя некоторые компоненты известны.

Поверхность Шерка является примером минимальной поверхности. Шерк описал две полные вложенные минимальные поверхности в 1834 году. Его первая поверхность является дважды периодической поверхностью, а вторая — просто периодической. Они были третьим нетривиальным примером минимальных поверхностей. Две поверхности сопряжены друг другу.

Минимальная поверхность Бура — двухмерная минимальная поверхность, вложенная с самопересечениями в трёхмерное евклидово пространство. Поверхность названа именем Эдмонда Бура, работа которого о минимальных поверхностях получила в 1861 году математический приз Французской академии наук.

В дифференциальной геометрии Минимальная поверхность Каталана — это минимальная поверхность, которую впервые исследовал Эжен Шарль Каталан в 1855 г..

Семейство поверхностей Чена — Гакстаттера — это семейство минимальных поверхностей, которое обобщает поверхность Эннепера путём добавления ручек, дающее поверхности ненулевой топологический род.
Минимальные поверхности Шварца — это периодические минимальные поверхности, первоначально описанные Карлом Шварцем.

Трижды периодическая минимальная поверхность — это минимальная поверхность в  , являющаяся инвариантом по переносам в решётке ранга 3.
, являющаяся инвариантом по переносам в решётке ранга 3.

Поверхности постоянной средней кривизны — класс поверхностей моделирующий поверхности мыльных плёнок разделяющие области с фиксированной разницей давлений. В частном случае, если давление с обеих сторон равно, модель определяет минимальные поверхности.
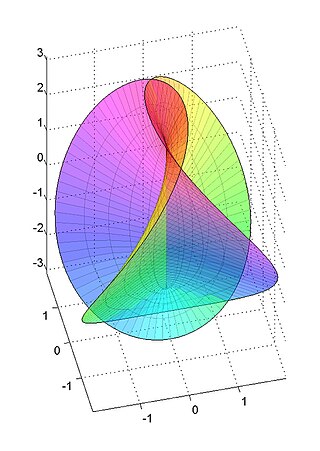
Поверхность Хеннеберга — неориентируемая минимальная поверхность, названная именем немецкого математика Лебрехта Хенненберга.
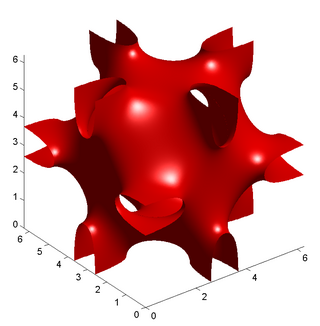
Поверхность Неовиуса — трижды периодическая минимальная поверхность, первоначально обнаруженная финским математиком Эдвардом Рудольфом Неовиусом.

Гироид — бесконечно связанная трижды периодическая минимальная поверхность, открытая Аланом Шоэном в 1970 году

Параметризация Вейерштрасса — Эннепера минимальных поверхностей — классический раздел дифференциальной геометрии.

Минимальная поверхность Косты — вложенная минимальная поверхность, обнаруженная в 1982 году бразильским математиком Селсо Жозе да Костой. Поверхность обладает конечной топологией, то есть она может быть образована проколом компактной поверхности. Топологически это трижды проколотый тор.
Эта страница основана на
статье Википедии.
Текст доступен на условиях лицензии
CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.























