Минимальная поверхность Шварца
Минимальные поверхности Шварца — это периодические минимальные поверхности, первоначально описанные Карлом Шварцем.
В 1880-х годах Шварц и его студент Е. Р. Неовиус описали периодические минимальные поверхности[1][2]. Им позднее дал названия Алан Шён в его фундаментальном отчёте, где он описал гироид и другие трижды периодические минимальные поверхности[3].
Поверхности генерировались с помощью симметрий: если дано решение задачи Плато для многоугольника, отражения поверхности относительно линий границы также даёт правильные минимальные поверхности, которые могут быть непрерывным образом соединены с исходным решением. Если минимальная поверхность встречает плоскость под прямыми углами, то зеркальное отражение относительно плоскости также может быть присоединено к поверхности. Следовательно, если дан подходящий начальный многоугольник, вписанный в единичную ячейку, периодическая поверхность может быть построена[4].
Поверхности Шварца имеют топологический род 3, минимальный род трижды периодических минимальных поверхностей[5].
Они рассматривались как модели для периодических наноструктур в блок-сополимерах, электростанических эквипотенциальных поверхностях в кристаллах[6] и гипотетических отрицательно искривлённых графитовых фазах[7].
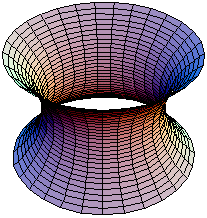
Поверхность Шварца P («Primitive» = «Примитивная»)

Шён назвал эти поверхности «примитивными», поскольку они имеют два переплетённых конгруэнтных лабиринта, каждый из которых имеет форму раздутой трубчатой версии простой кубической решётки. В то время как стандартная поверхность P имеет кубическую симметрию, ячейки могут иметь форму любого прямоугольника, что даёт семейство минимальных поверхностей с одной и той же топологией[8].
Поверхность можно аппроксимировать явной поверхностью
- [9].
Поверхность P рассматривалась для разработки прототипов тканевых каркасов с высоким отношением поверхности к объёму и высокой пористостью[10].
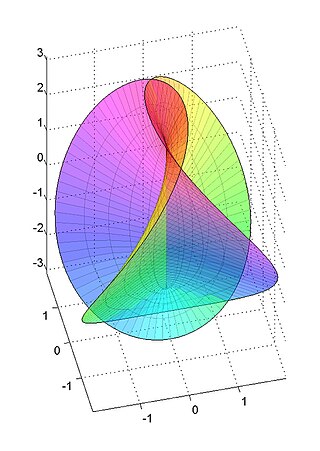
Поверхность Шварца D («Diamond» = «Алмаз»)

Шён назвал эту поверхность «алмазом», поскольку она имеет два переплетающихся конгруэнтных лабиринта, каждый из которых имеет форму раздутой полой версии алмазной структуры связи[англ.]. В литературе эта поверхность иногда называется поверхностью F.
Поверхность может быть аппроксимирована явной поверхностью
Точное выражение существует в терминах эллиптических интегралов, основанных на параметризации Вейерштрасса — Эннепера[11].
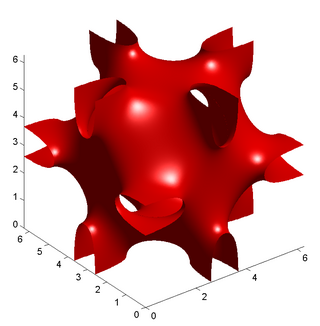
Поверхность Шварца H («Hexagonal» = «Шестиугольная»)

Поверхность Шварца H подобна катеноиду с треугольной границей, что позволяет заполнить всё пространство.
Поверхность Шварца CLP («Crossed layers of parallels» = «Скрещённые слои параллелей»)

Иллюстрации
- http://www.susqu.edu/brakke/evolver/examples/periodic/periodic.html
- Triply Periodic Surfaces of Genus 3
- Bicontinuous cubic phases based on triply periodic minimal surfaces
- Schwartz's Surface
- http://virtualmathmuseum.org/Surface/gallery_m.html
Примечания
- ↑ Schwarz, 1933.
- ↑ Neovius, 1883.
- ↑ Schoen, 1970.
- ↑ Karcher, Polthier, 1996, с. 2077–2104.
- ↑ Alan Schoen geometry. Дата обращения: 30 июля 2020. Архивировано 26 мая 2020 года.
- ↑ Mackay, 1985, с. 604–606.
- ↑ Terrones, Mackay, 1994, с. 183–195.
- ↑ Meeks, 1990, с. 77—936.
- ↑ Triply Periodic Level Surfaces. Дата обращения: 10 февраля 2019. Архивировано 12 февраля 2019 года.
- ↑ Shin, Kim, Jeong и др., 2012.
- ↑ Gandy, Cvijović, Mackay, Klinowski, 1999, с. 543–551.
Литература
- H. A. Schwarz. Gesammelte Mathematische Abhandlungen. — Berlin: Springer, 1933.
- E. R. Neovius. Akad. Abhandlungen. — Helsingfors, 1883.
- Alan H. Schoen. Infinite periodic minimal surfaces without self-intersections // NASA Technical Note TN D-5541. — 1970.
- Hermann Karcher, Konrad Polthier. Construction of Triply Periodic Minimal Surfaces // Phil. Trans. R. Soc. Lond. A. — 1996. — Сентябрь (т. 354, № 1715).
- Alan L. Mackay. Periodic minimal surfaces // Nature. — 1985. — Апрель (т. 314, № 6012). — doi:10.1038/314604a0.
- Terrones H., Mackay A. L. Negatively curved graphite and triply periodic minimal surfaces. — 1994. — Декабрь (вып. 15, № 1). — doi:10.1007/BF01277558.
- W. H. Meeks. The theory of triply-periodic minimal surfaces // Indiana University Math. Journal. — 1990. — Т. 39, вып. 3.
- Jaemin Shin, Sungki Kim, Darae Jeong, Hyun Geun Lee, Dongsun Lee, Joong Yeon Lim, Junseok Kim. Finite Element Analysis of Schwarz P Surface Pore Geometries for Tissue-Engineered Scaffolds // Mathematical Problems in Engineering. — 2012. — doi:10.1155/2012/694194.
- Paul J.F. Gandy, Djurdje Cvijović, Alan L. Mackay, Jacek Klinowski. Exact computation of the triply periodic D (`diamond') minimal surface // Chemical Physics Letters. — 1999. — Декабрь (т. 314, вып. 5–6, 10).