Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством разнообразных вычислений. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач. Современная вычислительная математика включает в круг своих проблем изучение особенностей вычисления с применением компьютеров.
Лине́йная а́лгебра — раздел алгебры, изучающий математические объекты линейной природы: векторные пространства, линейные отображения, системы линейных уравнений. Среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно также считаются составными частями линейной алгебры. Такие объекты как квадратичные и билинейные формы, тензоры и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.
Основна́я теоре́ма а́лгебры — утверждение о том, что поле комплексных чисел алгебраически замкнуто, то есть что всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел. Утверждение справедливо и для многочленов с вещественными коэффициентами, так как всякое вещественное число является комплексным с нулевой мнимой частью.
Жорданова матрица — квадратная блочно-диагональная матрица над полем 
, с блоками вида
А́ртур Кэ́ли — английский математик, профессор Кембриджского университета. Член Лондонского королевского общества (1852), член-корреспондент Петербургской академии наук (1870), иностранный член Парижской академии наук, Королевской академии наук и искусств Нидерландов (1893) и ряда других академий. Президент Лондонского математического общества (1868–1870). Лауреат медали Копли (1862) и медали де Моргана (1884).
Характеристический многочлен матрицы — многочлен, определяющий её собственные значения.
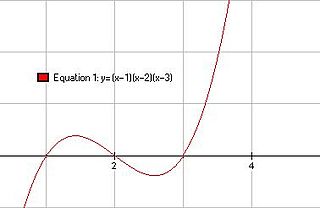
Корень многочлена
Со́бственный ве́ктор — понятие в линейной алгебре, определяемое для произвольного линейного оператора как ненулевой вектор, применение к которому оператора даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение. Скаляр, на который умножается собственный вектор под действием оператора, называется собственным числом линейного оператора, соответствующим данному собственному вектору. Одним из представлений линейного оператора является квадратная матрица, поэтому собственные векторы и собственные значения часто определяются в контексте использования таких матриц.
Λ, λ — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы 𐤋 — ламд. От буквы лямбда произошли латинская буква L и кириллическая Л, а также их производные.
В линейной алгебре, фробениусовой нормальной формой линейного оператора А называется каноническая форма его матрицы, соответствующая минимальному разложению линейного пространства в прямую сумму инвариантных относительно А подпространств, которые могут быть получены как линейная оболочка некоторого вектора и его образов под действием А. Она будет блочно-диагональной матрицей, состоящей из фробениусовых клеток вида
Аннули́рующий многочле́н для ма́трицы — многочлен 
, значение которого для данной квадратной матрицы 
равно нулевой матрице. Теорема Гамильтона-Кэли утверждает, что значение характеристического многочлена для квадратной матрицы равно нулевой матрице, а значит для каждой квадратной матрицы существует, по крайней мере, один аннулирующий многочлен степени, совпадающей с порядком матрицы.
Теоре́ма Га́мильтона — Кэ́ли — классическая теорема линейной алгебры, утверждает, что любая квадратная матрица удовлетворяет своему характеристическому уравнению. Названная в честь Уильяма Гамильтона и Артура Кэли.
Численные (вычислительные) методы — методы решения математических задач в численном виде.
В алгебре комплексных чисел приведённый многочлен — это многочлен одной переменной с единичным старшим коэффициентом. Старшим коэффициентом многочлена называется множитель при одночлене высшей степени. Соответственно, приведённый многочлен относительно одной переменной x имеет вид
где an−1, …, a0 — коэффициенты.
В настоящее время отсутствует единое определение точно решаемой задачи для всех разделов математики. Это обусловлено особенностями самих задач и методов поиска их решения. Вместе с тем базовые теоремы, определяющие наличие и единственность решений, строятся на общих принципах, что будет показано ниже.
Структурная теорема для конечнопорождённых модулей над областями главных идеалов является обобщением теоремы о классификации конечнопорождённых абелевых групп. Эта теорема предоставляет общий способ понимания некоторых результатов о канонических формах матриц.
Нормальная форма Смита — это диагональная матрица над областью главных идеалов, каждый следующий диагональный элемент которой делится на предыдущий. Любую матрицу над областью главных идеалов можно привести к нормальной форме Смита путём умножения слева и справа на обратимые матрицы.
Алгебраическая теория графов — направление в теории графов, применяющее алгебраические методы к теоретико-графовым задачам. В свою очередь, алгебраическая теория графов подразделяется на три ветви: линейно-алгебраическую, теоретико-групповую и изучающую инварианты графов.
