Ме́ра мно́жества — числовая характеристика множества, интуитивно её можно понимать как массу множества при некотором распределении массы по пространству. Понятие меры множества возникло в теории функций вещественной переменной при развитии понятия интеграла.
Сложе́ние (прибавле́ние) — одна из основных бинарных математических операций двух аргументов (слагаемых), результатом которой является новое число (сумма), получаемое увеличением значения первого аргумента на значение второго аргумента. То есть каждой паре элементов 
из множества 
ставится в соответствие элемент 
, называемый суммой 
и 
. Это одна из четырёх элементарных математических операций арифметики. Приоритет её в обычном порядке операций равен приоритету вычитания, но ниже, чем у возведения в степень, извлечения корня, умножения и деления. На письме сложение обычно обозначается с помощью знака «плюс»: 
.
Сложение возможно, только если оба аргумента принадлежат одному множеству элементов. Так, на картинке справа запись 
обозначает три яблока и два яблока вместе, что в сумме даёт пять яблок. Но нельзя сложить, например, 3 яблока и 2 груши.
Вычита́ние (убавление) — одна из вспомогательных бинарных математических операций двух аргументов, результатом которой является новое число (разность), получаемое уменьшением значения первого аргумента на значение второго аргумента. На письме обычно обозначается с помощью знака «минус»: 
. Вычитание — операция обратная сложению.
Предика́т — это утверждение, высказанное о субъекте. Субъектом высказывания называется то, о чём делается утверждение. В лингвистике субъекту соответствует подлежащее, а предикату — сказуемое.
Фу́нкция — соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого.
В этой статье приведены основные термины, используемые в теории групп. Курсив обозначает внутреннюю ссылку на данный глоссарий. В конце приводится таблица основных обозначений, применяемых в теории групп.
Конъю́нкция — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум .
Вариацио́нное исчисле́ние — раздел анализа, в котором изучаются вариации функционалов. Наиболее типичная задача — найти функцию, на которой заданный функционал достигает экстремального значения.
Точная верхняя граница и точная нижняя граница — обобщение понятий максимума и минимума множества соответственно.
Усло́вный экстре́мум — максимальное или минимальное значение, которое функция, определённая на множестве 
и принимающая вещественные значения, достигает в предположении, что значения некоторых других функций с той же областью определения подчинены определённым ограничительным условиям.
Точка перегиба — точка плоской кривой, в которой её ориентированная кривизна меняет знак. Если кривая является графиком функции, то в этой точке выпуклая часть функции отделяется от вогнутой.
Оптимизация — задача нахождения экстремума целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств или неравенств.
Периодическая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа на всей области определения.
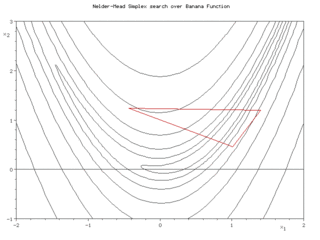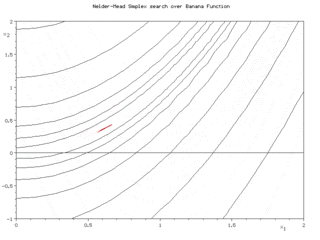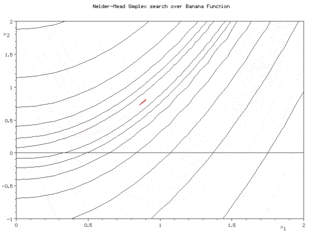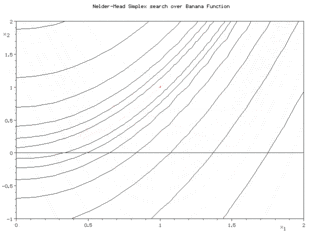
Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной функции, а поэтому легко применим к негладким и/или зашумлённым функциям.
Поворот Вика — метод решения задач в пространстве Минковского посредством решения связанной задачи в евклидовом пространстве, используя комплексный анализ, в частности, понятие аналитического продолжения. Назван в честь Джанкарло Вика.
EMD — метод разложения сигналов на функции, которые получили название «эмпирических мод».
