
Пространство Кала́би — Яу — компактное комплексное многообразие с кэлеровой метрикой, для которой тензор Риччи обращается в ноль. В теории суперструн иногда предполагают, что дополнительные измерения пространства-времени принимают форму 6-мерного многообразия Калаби — Яу, что привело к идее зеркальной симметрии. Название было придумано в 1985 году, в честь Эудженио Калаби, который впервые предположил, что такие размерности могут существовать, и Яу Шинтуна, который в 1978 году доказал гипотезу Калаби.

Уравне́ния Эйнште́йна — уравнения гравитационного поля, лежащие в основе общей теории относительности, связывающие между собой компоненты метрического тензора  искривлённого пространства-времени с компонентами тензора энергии-импульса материи, заполняющей пространство-время. Термин используется и в единственном числе: «уравне́ние Эйнште́йна», так как в тензорной записи это одно уравнение, хотя в компонентах представляет собой систему нелинейных дифференциальных уравнений в частных производных.
искривлённого пространства-времени с компонентами тензора энергии-импульса материи, заполняющей пространство-время. Термин используется и в единственном числе: «уравне́ние Эйнште́йна», так как в тензорной записи это одно уравнение, хотя в компонентах представляет собой систему нелинейных дифференциальных уравнений в частных производных.
Риманов тензор кривизны представляет собой стандартный способ выражения кривизны римановых многообразий, а в общем случае — произвольных многообразий аффинной связности, без кручения или с кручением.
Космологи́ческая постоя́нная, иногда называемая лямбда-член — физическая постоянная, характеризующая свойства вакуума, которая вводится в общей теории относительности. С учётом космологической постоянной уравнения Эйнштейна имеют вид

Те́нзор эне́ргии-и́мпульса (ТЭИ) — симметричный тензор второго ранга (валентности), описывающий плотность и поток энергии и импульса полей материи и определяющий взаимодействие этих полей с гравитационным полем.
Тензор кривизны Вейля — часть тензора кривизны Римана с нулевым следом. Другими словами, это тензор, удовлетворяющий всем свойствам симметрии тензора Римана с дополнительным условием, что построенный по нему тензор Риччи равен нулю.
Теория Калуцы — Клейна — одна из многомерных теорий гравитации, позволяющая объединить два фундаментальных физических взаимодействия: гравитацию и электромагнетизм. Теория была впервые опубликована в 1921 году немецким математиком Теодором Калуцей, который расширил пространство Минковского до 5-мерного пространства и получил из уравнений своей теории уравнения общей теории относительности и классические уравнения Максвелла. Обоснование ненаблюдаемости пятого измерения было предложено шведским физиком Оскаром Клейном в 1926 году.
Тензор Риччи, названный в честь итальянского математика Грегорио Риччи-Курбастро, задаёт один из способов измерения кривизны многообразия, то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства. Тензор Риччи, точно так же как метрический тензор, является симметричной билинейной формой на касательном пространстве риманова многообразия. Грубо говоря, тензор Риччи измеряет деформацию объёма, то есть степень отличия n-мерных областей n-мерного многообразия от аналогичных областей евклидова пространства (см. геометрический смысл тензора Риччи). Обычно обозначается  или
или  .
.
Вселе́нная Фри́дмана — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.
Поток Риччи — система дифференциальных уравнений в частных производных, описывающая деформацию римановой метрики на многообразии.
Эйнште́йновский ва́куум — иногда встречающееся название для решений уравнений Эйнштейна в общей теории относительности для пустого, без материи, пространства-времени. Синоним — пространство Эйнштейна.
Кру́чение аффи́нной свя́зности — одна из геометрических характеристик связностей в дифференциальной геометрии. В отличие от понятия кривизны, имеющего смысл для связности в произвольном векторном расслоении или даже связности Эресманна в локально тривиальном расслоении, кручение может быть определено лишь для связностей в касательном расслоении.
Решить уравнение Эйнштейна — значит, найти вид метрического тензора  пространства-времени. Задача ставится заданием граничных условий, координатных условий и написанием тензора энергии-импульса
пространства-времени. Задача ставится заданием граничных условий, координатных условий и написанием тензора энергии-импульса  , который может описывать как точечный массивный объект, распределённую материю или энергию, так и всю Вселенную целиком. В зависимости от вида тензора энергии-импульса решения уравнения Эйнштейна можно разделить на вакуумные, полевые, распределённые, космологические и волновые. Существуют также чисто математические классификации решений, основанные на топологических или алгебраических свойствах описываемого ими пространства-времени, или, например, на алгебраической симметрии тензора Вейля данного пространства.
, который может описывать как точечный массивный объект, распределённую материю или энергию, так и всю Вселенную целиком. В зависимости от вида тензора энергии-импульса решения уравнения Эйнштейна можно разделить на вакуумные, полевые, распределённые, космологические и волновые. Существуют также чисто математические классификации решений, основанные на топологических или алгебраических свойствах описываемого ими пространства-времени, или, например, на алгебраической симметрии тензора Вейля данного пространства.
Скалярная кривизна — один из инвариантов риманова многообразия, получаемый свёрткой тензора Риччи с метрическим тензором. Обычно обозначается  или
или  .
.
Разложение Риччи — это разложение тензора кривизны Римана на неприводимые относительно ортогональной группы тензорные части. Это разложение играет важную роль в римановой и псевдоримановой геометрии.
Теория Эйнштейна — Картана (ЭК) была разработана как расширение общей теории относительности, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина материальных полей. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен общей теории относительности, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к общей теории относительности в условиях современной Вселенной настолько малы, что пока не видно даже гипотетических путей для их измерения.
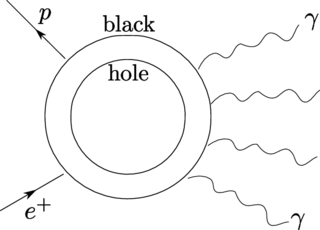
Виртуальная чёрная дыра — гипотетический объект квантовой гравитации: чёрная дыра, возникшая в результате квантовой флуктуации пространства-времени. Является одним из примеров так называемой квантовой пены и гравитационным аналогом виртуальных электрон-позитронных пар в квантовой электродинамике.
Неравенство Бишопа — Громова — теорема сравнения в римановой геометрии. Является ключевым утверждением в доказательстве теоремы Громова о компактности.

Кривизна римановых многообразий численно характеризует отличие римановой метрики многообразия от евклидовой в данной точке.
Риччи-солитон — решение потока Риччи при котором пространство не меняется или меняется только изменением масштаба. Названы в честь Грегорио Риччи-Курбастро.























