Геоме́трия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. В практических задачах геометрия позволяет предсказывать геометрические размеры тела, зная другие геометрические размеры этого тела с помощью известных геометрических законов.

, в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы. Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

Стереографи́ческая проекция — отображение определённого типа из сферы с одной выколотой точкой на плоскость.

Бесконе́чность — категория человеческого мышления, используемая для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, для которых невозможно указание границ или количественной меры. Используется в противоположность конечному, исчисляемому, имеющему предел. Систематически исследуется в математике, логике и философии, также изучаются вопросы о восприятии, статусе и природе бесконечности в психологии, теологии, физике соответственно. Бесконечность обозначается символом  .
.

Ве́ктор — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве.

Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.

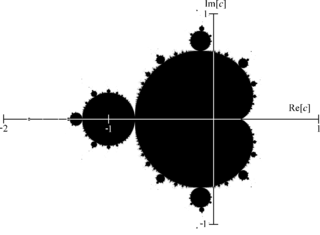
Фракта́л — множество, обладающее свойством самоподобия. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.

То́чка — один из фундаментальных (неопределяемых) математических объектов, свойства которого задаются системой аксиом. Нестрого можно представлять точку как неделимый элемент соответствующего математического пространства, определяемого в геометрии, математическом анализе и других разделах математики. В классической геометрии и в большинстве её обобщений все геометрические фигуры считаются состоящими из точек.
Многообра́зие — локально евклидово пространство.
Осева́я симме́три́я — тип симметрии, имеющий несколько отличающихся определений:
- Отражение. В евклидовой геометрии осевая симметрия — вид движения, при котором множеством неподвижных точек является прямая, называемая осью симметрии. Отсюда следует, что любой точке соответствует точка, находящаяся на том же расстоянии от оси симметрии, и лежащая на одной прямой с исходной точкой и их общей проекцией на ось симметрии. Например, плоская фигура параллелограмм в пространстве осесимметрична и имеет одну ось симметрии, а его частный случай, прямоугольник, в пространстве имеет уже 3 оси симметрии.
- Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию относительно поворотов вокруг прямой. При этом тело называют осесимметричными, если они переходят в себя при любом повороте вокруг этой прямой. В этом случае прямоугольник не будет осесимметричным телом, но, например, конус будет.

Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Конечная геометрия — геометрическая система, имеющая конечное количество точек. Например, евклидова геометрия не является конечной, так как евклидова прямая содержит неограниченное число точек, а точнее говоря, содержит ровно столько точек, сколько существует вещественных чисел. Конечная геометрия может иметь любое конечное число измерений.

Алгебраическое многообразие — центральный объект изучения алгебраической геометрии. Классическое определение алгебраического многообразия — множество решений системы алгебраических уравнений над действительными или комплексными числами. Современные определения обобщают его различными способами, но стараются сохранить геометрическую интуицию, соответствующую этому определению.
Группа симметрии некоторого объекта ― группа всех преобразований, для которых данный объект является инвариантом, с композицией в качестве групповой операции. Как правило, рассматриваются множества точек n-мерного евклидова пространства и движения этого пространства, но понятие группы симметрии сохраняет свой смысл и в более общих случаях.

Задача со счастливым концом — утверждение о том, что любое множество из пяти точек на плоскости в общем положении имеет подмножество из четырёх точек, которые являются вершинами выпуклого четырёхугольника.

В теории графов графом единичных расстояний называется граф, образованный точками на евклидовой плоскости, при этом две вершины соединяются ребром, если расстояние между ними равно в точности единице. Рёбра графа единичных расстояний иногда пересекаются, так что они не всегда планарны. Граф единичных расстояний без пересечений называется спичечным графом.

Задача об иголке состоит в определении минимальной площади фигуры на плоскости, в которой единичный отрезок, «иглу», можно развернуть на 180 градусов, вернув его в исходное положение с обращённой ориентацией. Такое возможно проделать в круге радиуса 1/2. Другой пример — фигура, ограниченная дельтоидой, — показан на картинке, он имеет меньшую площадь.

Апериодичная мозаика — это непериодичное замощение с дополнительным свойством, что замощение не содержит бесконечно больших периодических кусков. Множество типов плиток является набором непериодичных протоплиток, если копии этих плиток могут образовать только апериодичные мозаики. Мозаики Пенроуза являются наиболее известными примерами апериодичных мозаик.