Аналитическое продолжение в комплексном анализе — аналитическая функция, совпадающая с заданной функцией  в её исходной области C и определённая при этом в области D, содержащей C — продолжение функции
в её исходной области C и определённая при этом в области D, содержащей C — продолжение функции  , являющееся аналитическим. Аналитическое продолжение всегда единственно.
, являющееся аналитическим. Аналитическое продолжение всегда единственно.

Ориента́ция — обобщение и формализация понятий направления обхода и направления на прямой на более сложные геометрические объекты, многообразия, векторные расслоения и так далее.
Теорема Хопфа — Ринова — теорема дифференциальной геометрии, доказанная Хайнцем Хопфом и его учеником Вилли Риновым. Опубликована последним в 1931 году.

Геодези́ческая — кривая определённого типа, обобщение понятия «прямая» для искривлённых пространств.
Внутренняя метрика — метрика в пространстве, определяемая с помощью функционала длины, как инфимум длин всех путей (кривых), соединяющих данную пару точек.

Задача Штейнера о минимальном дереве состоит в поиске кратчайшей сети, соединяющей заданный конечный набор точек плоскости. Задача получила своё название в честь Якоба Штейнера (1796—1863).

Выпуклые метрические пространства интуитивно определяются как метрические пространства с таким свойством, что любой «отрезок», который соединяет две точки этого пространства, содержит другие точки, кроме своих концов.
Лемма Маргулиса — одно из ключевых утверждений об изометрических действиях на римановых многообразиях.
Теорема сравнения Топоногова — классическая теорема римановой геометрии в целом.
Теорема сравнения Рауха — фундаментальный результат римановой геометрии. Доказана Раухом.
Сопряжённые точки — вершины инфинитезимально узкого геодезического двуугольника в Римановом многообразии.
Замкнутая геодезическая на римановом многообразии — это геодезическая, которая образует простую замкнутую кривую. Её можно формализовать как проекцию замкнутой орбиты геодезического потока на касательное пространство многообразия.
Модулярная кривая  — это риманова поверхность или соответствующая алгебраическая кривая, построенная как фактор комплексной верхней половины плоскости H по конгруэнтной подгруппе
— это риманова поверхность или соответствующая алгебраическая кривая, построенная как фактор комплексной верхней половины плоскости H по конгруэнтной подгруппе  модулярной группы целочисленных 2×2 матриц SL(2, Z). Термин модулярная кривая может также использоваться для ссылок на компактифицированные модулярные кривые
модулярной группы целочисленных 2×2 матриц SL(2, Z). Термин модулярная кривая может также использоваться для ссылок на компактифицированные модулярные кривые  , которые являются компактификациями, полученными добавлением конечного числа точек к фактору. Точки модулярной кривой параметризуют классы изоморфизмов эллиптических кривых, вместе с некоторой дополнительной структурой, зависящей от группы
, которые являются компактификациями, полученными добавлением конечного числа точек к фактору. Точки модулярной кривой параметризуют классы изоморфизмов эллиптических кривых, вместе с некоторой дополнительной структурой, зависящей от группы  . Эта интерпретация позволяет дать чисто алгебраическое определение модулярных кривых без ссылок на комплексные числа, и, более того, доказывает, что модулярные кривые являются полем определения либо над полем Q рациональных чисел, либо над круговым полем. Последний факт и его обобщения имеют фундаментальную важность в теории чисел.
. Эта интерпретация позволяет дать чисто алгебраическое определение модулярных кривых без ссылок на комплексные числа, и, более того, доказывает, что модулярные кривые являются полем определения либо над полем Q рациональных чисел, либо над круговым полем. Последний факт и его обобщения имеют фундаментальную важность в теории чисел.
Фуксова модель — это представление гиперболической римановой поверхности R как факторповерхности верхней полуплоскости H по фуксовой группе. Любая гиперболическая риманова поверхность позволяет такое представление. Концепция названа именем Лазаря Фукса.
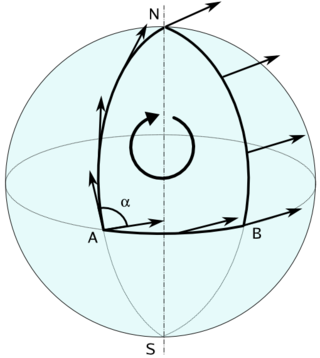
Голоно́ми́я — один из инвариантов связности в расслоении над гладким многообразием, сочетающий свойства кривизны и монодромии, и имеющий важное значение как в геометрии, так и геометризированных областях естествознания, таких как теория относительности и теория струн. Обыкновенно речь идёт о голономии связностей в векторном расслоении, хотя в равной степени имеет смысл говорить о голономии связности в главном расслоении или даже голономии связности Эресманна в локально тривиальном топологическом расслоении.