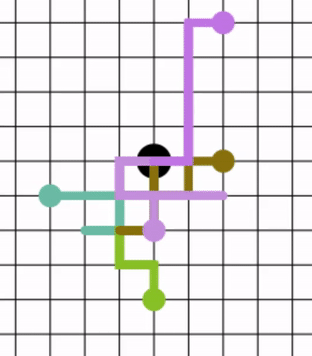
Случайное блуждание — математический объект, известный как стохастический или случайный процесс, который описывает путь, состоящий из последовательности случайных шагов в каком-нибудь математическом пространстве.

NGC 300 — спиральная галактика из группы галактик в созвездии Скульптор, также известная как Caldwell 70.
PGC 74886 — карликовая линзообразная галактика из каталога PGC, расположенная в группе 250 карликовых галактик. Галактика находится в созвездии Эридан, в ≈70 млн св. лет от Земли. Это первая известная галактика, имеющая форму округлого прямоугольника. Необычная галактика была совершенно случайно обнаружена суинбернским астрофизиком Ли Спитлером с помощью японского телескопа «Субару». Сначала авторы исследования предполагали, что форма LEDA 074886 объясняется взаимодействием с галактикой-соседом. Анализ окружения галактики, однако, позволил установить, что форма, скорее всего, объясняется тем, что новая галактика — результат столкновения двух карликовых соседей NGC 1407.

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.

Пятиугольный паркет — в геометрии: замощение, составленное из выпуклых пятиугольников. Замощение из правильных пятиугольников в евклидовом пространстве невозможно, поскольку общий угол правильного пятиугольника равен 108° и не делит ни 180°, ни 360°. Однако ими можно замостить гиперболическую плоскость и сферу.
Задача одной плитки — решённая геометрическая проблема поиска одной протоплитки, которая образует непериодическое множество плиток, то есть фигуры, копиями которой можно замостить плоскость, но только непериодичным способом.

Замощение плитками домино области в евклидовой плоскости — мозаика из плиток домино, которые образованы объединением двух единичных квадратов, соединённых по ребру. Эквивалентно — это паросочетание в графе решётки, образованное помещением вершины в центр каждого квадрата области и соединением двух вершин, если два соответствующих квадрата смежны.

Замощения евклидовой плоскости выпуклыми правильными многоугольниками широко использовался ещё с античных времён. Первое систематическое изложение было сделано Кеплером в его книге Harmonices Mundi.

Ромбическая мозаика, кантующиеся блоки, обратимые кубы или кубическая решётка — мозаика одинаковых ромбов с углом 60° на евклидовой плоскости. Каждый ромб имеет два угла 60° и два 120°. Такие ромбы иногда называют диамондами. Множества из трёх ромбов соприкасаются вершинами с углом 120°, а множества из шести — вершинами с углом 60°.
Задачи упаковки — это класс задач оптимизации в математике, в которых пытаются упаковать объекты в контейнеры. Цель упаковки — либо упаковать отдельный контейнер как можно плотнее, либо упаковать все объекты, использовав как можно меньше контейнеров. Многие из таких задач могут относиться к упаковке предметов в реальной жизни, вопросам складирования и транспортировки. Каждая задача упаковки имеет двойственную задачу о покрытии, в которой спрашивается, как много требуется некоторых предметов, чтобы полностью покрыть все области контейнера, при этом предметы могут накладываться.

Тришестиугольная мозаика — одна из 11 однородных мозаик на евклидовой плоскости из правильных многоугольников. Мозаика состоит из правильных треугольников и правильных шестиугольников, расположенных так, что каждый шестиугольник окружён треугольниками, и наоборот. Название мозаики вызвано тем фактом, что она комбинирует правильную шестиугольную мозаику и правильную треугольную мозаику. Два шестиугольника и два треугольника чередуются вокруг каждой вершины, а рёбра образуют бесконечную конфигурацию прямых. Двойственная мозаика — ромбическая.

Плитка Соколара — Тейлор — это одиночная плитка, которая апериодична на плоскости, что означает, что возможны только непериодичные замощения на плоскости при разрешении вращения и зеркального отражения. Плитка была первым примером одиночной апериодичной плитки, или «einstein». Плитка Соколара — Тейлор строится на основе правильного шестиугольника с некоторым узором для обеспечения локального правила соединения. Чтобы реализовать это локальное правило без условий на узор, плитка является несвязной, так как это правило не может быть геометрически реализовано в двухмерном пространстве в виде связной плитки. Из-за этого, для полного решения «Задачи одной плитки» в двумерном пространстве потребовались другие техники.
Оптимизация гиперпараметров — задача машинного обучения по выбору набора оптимальных гиперпараметров для обучающего алгоритма.
Выбор модели — это задача выбора статистической модели из набора моделей-кандидатов по имеющимся данным. В простейшем случае рассматривается существующий набор данных. Однако задача может вовлекать планирование экспериментов, так что сбор данных связан с задачей выбора модели. Если заданы кандидаты в модели с одинаковой силой предсказания или объяснения, наиболее простая модель скорее всего будет лучшим выбором.

В статистике методы Монте-Карло с марковскими цепями (англ. MCMC) — это класс алгоритмов для семплирования, моделирующих некоторое распределение вероятностей. Построив марковскую цепь, которая имеет целевое распределение в качестве своего равновесного, можно получить выборку с тем же распределением путем записи состояний цепи. Чем больше шагов будет использовано, тем ближе распределение выборки будет к целевому. Для построения цепей используются различные алгоритмы, например, алгоритм Метрополиса-Гастингса.
Кси Возничего, 30 Возничего, 32 Жирафа, HD 39283 — одиночная звезда в созвездии Возничего на расстоянии приблизительно 236 световых лет от Солнца. Видимая звёздная величина звезды — +4,96m. Возраст звезды оценивается как около 174 млн лет.
14 Волос Вероники, HD 108283 — двойная звезда в созвездии Волос Вероники на расстоянии приблизительно 266 световых лет от Солнца. Видимая звёздная величина звезды — +4,95m. Возраст звезды определён как около 459 млн лет.
39 Волос Вероники, HD 113848 — тройная звезда в созвездии Волос Вероники на расстоянии приблизительно 162 световых лет от Солнца. Возраст звезды определён как около 1,361 млрд лет.





















