Квадри́рование квадра́та — задача о разбиении квадрата на конечное число меньших квадратов. В более узком смысле — задача о разбиении квадрата на конечное число попарно неравных между собой квадратов.
Странное число — натуральное число, которое является избыточным, но не является полусовершенным. Другими словами, сумма собственных делителей числа больше самого числа, но сложением подмножества делителей нельзя получить само число.
Полимино, или полиомино — плоские геометрические фигуры, образованные путём соединения нескольких одноклеточных квадратов по их сторонам. Это полиформы, сегменты которых являются квадратами.
Полиамонд или треуго́льный мо́нстр — геометрическая фигура в виде многоугольника, составленного из нескольких одинаковых равносторонних треугольников, примыкающих друг к другу по рёбрам. Полиамонды можно рассматривать как конечные подмножества треугольного паркета со связной внутренностью.
Гептамино — семиклеточное полимино, то есть плоская фигура, состоящая из семи равных квадратов, соединённых сторонами. С фигурами гептамино, как со всеми полимино, связано много задач занимательной математики.
Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.
Квадра́тный парке́т, квадратный паркетаж, квадратная мозаика или квадратная решётка — это замощение плоскости равными квадратами, расположенными сторона к стороне, при этом вершины четырёх смежных квадратов находятся в одной точке. Символ Шлефли мозаики — {4,4}, означающий, что вокруг каждой вершины имеется 4 квадрата.
Куб принца Руперта — задача, заключающееся в том, что в нём можно проделать отверстие, через которое возможно протащить копию изначального куба. Ребро куба Руперта приблизительно на 6 % длиннее, чем ребро куба, через который он проходит. Задача поиска такого куба тесно связана с задачей поиска самого большего квадрата, который полностью расположен в пределах единичного куба, и имеет аналогичное решение.
Нонамино — девятиклеточные полимино, или многоугольники, составленные из 9 равных квадратов, соединённых сторонами.
Декамино — десятиклеточные полимино, или многоугольники, составленные из 10 единичных квадратов, соединённых сторонами.
Делящаяся плитка — понятие геометрии мозаик, фигура, которую можно разрезать на меньшие копии самой фигуры. В 2012 обобщение делящихся мозаик с названием self-tiling tile set было предложено английским математиком Ли Сэлоусом в журнале Mathematics Magazine.
Замощение плитками домино области в евклидовой плоскости — мозаика из плиток домино, которые образованы объединением двух единичных квадратов, соединённых по ребру. Эквивалентно — это паросочетание в графе решётки, образованное помещением вершины в центр каждого квадрата области и соединением двух вершин, если два соответствующих квадрата смежны.
Набор плиток с самозамощением порядка n — это набор из n фигур, обычно плоских, каждая из которых допускает замощение меньшими копиями тех же n фигур. Более точно, n фигур могут быть собраны n различными способами, дающими большие копии фигур из того же набора, и коэффициент увеличения один и тот же. Рисунок 1 показывает пример для n = 4 с использованием декамино различной формы. Концепцию можно обобщить и использовать фигуры большей размерности. Название setisets дал Ли Сэллоус в 2012 году, но задача нахождения таких наборов для n = 4 поставил задолго до этого Дадли Лэнгфорд, а примеры для фигур полиаболо и полимино опубликованы до этого Гарднером.
Пифагорова мозаика — замощение евклидовой плоскости квадратами двух различных размеров, в которой каждый квадрат касается четырёх квадратов другого размера своими четырьмя сторонами. Исходя из этой мозаики, можно доказать (наглядно) теорему Пифагора, за что мозаика и получила название пифагоровой. Мозаика часто используется в качестве узора для кафельного пола. В этом контексте мозаика известна также как узор классов.
Задачи упаковки — это класс задач оптимизации в математике, в которых пытаются упаковать объекты в контейнеры. Цель упаковки — либо упаковать отдельный контейнер как можно плотнее, либо упаковать все объекты, использовав как можно меньше контейнеров. Многие из таких задач могут относиться к упаковке предметов в реальной жизни, вопросам складирования и транспортировки. Каждая задача упаковки имеет двойственную задачу о покрытии, в которой спрашивается, как много требуется некоторых предметов, чтобы полностью покрыть все области контейнера, при этом предметы могут накладываться.
Изогональный или вершинно транзитивный многогранник — многогранник, все вершины которого эквивалентны. В частности все вершины окружены одним и тем же видом граней в том же самом порядке и с теми же самыми углами между соответствующими гранями. Термин также может быть применён к многоугольникам или замощениям и так далее.
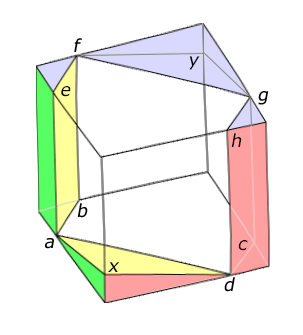
Критерий Конвея — набор условий, при выполнении которых протоплитка замощает плоскость. Назван по имени английского математика Джона Хортона Конвея. Выполнение критерия Конвея является достаточным, но не обязателеным условием для замощения плоскости.
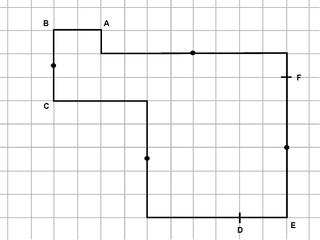
Разбиение многоугольника — это множество примитивных элементов, которые не накладываются и объединение которых равно многоугольнику. Задача о разбиении многоугольника — это задача поиска разбиения, которое в некотором смысле минимально, например, разбиение с наименьшим числом элементов или разбиение с наименьшей суммой длин сторон.
Апериодичная мозаика — это непериодичное замощение с дополнительным свойством, что замощение не содержит бесконечно больших периодических кусков. Множество типов плиток является набором непериодичных протоплиток, если копии этих плиток могут образовать только апериодичные мозаики. Мозаики Пенроуза являются наиболее известными примерами апериодичных мозаик.
Journal of Recreational Mathematics — американский журнал, посвящённый занимательной математике. Основан в 1968 году, закрыт в 2014 году. Выходил, за редким исключением, ежеквартально. Начальные тома (1—5) были изданы компанией Greenwood Publishing Group, далее изданием занималась Baywood Publishing Company.
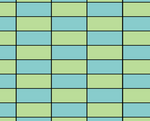Сложенная облигация 
Бегущая связь 
Плетение корзины 
Плетение корзины 
Узор "ёлочка" 