
Тео́рия гра́фов — раздел дискретной математики, изучающий графы, одна из ветвей топологии. В самом общем смысле граф — это множество точек, которые соединяются множеством линий. Теория графов включена в учебные программы для начинающих математиков, поскольку:
- как и геометрия, обладает наглядностью;
- как и теория чисел, проста в объяснении и имеет сложные нерешённые задачи;
- не имеет громоздкого математического аппарата ;
- имеет выраженный прикладной характер.
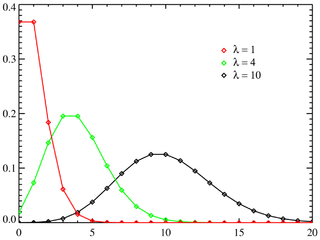
Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Преобразова́ние Лапла́са (ℒ) — интегральное преобразование, связывающее функцию  комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией  вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Уильям Сили Госсет первым опубликовал работы, посвящённые этому распределению, под псевдонимом «Стьюдент».

Зако́н Сте́фана — Бо́льцмана — интегральный закон излучения абсолютно чёрного тела. Он определяет зависимость плотности мощности излучения абсолютно чёрного тела от его температуры. В словесной форме его можно сформулировать следующим образом:
Полная объёмная плотность равновесного излучения и полная испускательная способность абсолютно чёрного тела пропорциональны четвёртой степени его температуры.

Фо́рмула Пла́нка — формула, описывающая спектральную плотность излучения, которое создаётся абсолютно чёрным телом определённой температуры. Формула была открыта Максом Планком в 1900 году и названа по его фамилии. Её открытие сопровождалось появлением гипотезы о том, что энергия может принимать только дискретные значения. Эта гипотеза некоторое время после открытия не считалась значимой, но, как принято считать, дала рождение квантовой физике.
Квазичастицы в графене обладают линейным законом дисперсии вблизи дираковских точек и их свойства полностью описываются уравнением Дирака. Сами дираковские точки находятся на краях зоны Бриллюэна, где электроны обладают большим волновым вектором. Если пренебречь процессами переброса между долинами, то этот большой вектор никак не влияет на транспорт в низкоэнергетическом приближении, поэтому волновой вектор, фигурирующий в уравнении Дирака, отсчитывают от дираковских точек и уравнение Дирака записывают для разных долин отдельно.
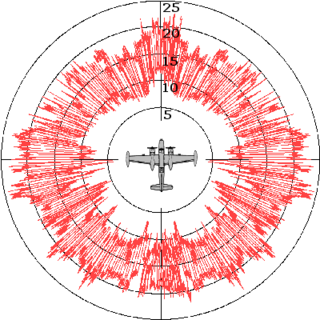
Эффекти́вная пло́щадь рассе́яния в радиолокации — площадь некоторой фиктивной плоской поверхности, расположенной нормально к направлению падающей плоской волны и являющейся идеальным и изотропным переизлучателем, которая, будучи помещена в точку расположения цели, создаёт в месте расположения антенны радиолокационной станции ту же плотность потока мощности, что и реальная цель.
Тепловые флуктуации приводят к тому, что на поверхности жидкости постоянно генерируются капиллярные волны, которые оказывают значительное влияние на структуру поверхностного слоя жидкости.
SQUARE — в криптографии симметричный блочный криптоалгоритм, разработанный в 1997 году Винсентом Рэйменом, Йоаном Дайменом и Ларсом Кнудсеном.
Теорема Дирихле о единицах — теорема алгебраической теории чисел, описывающая ранг подгруппы обратимых элементов кольца алгебраических целых  числового поля
числового поля  .
.
Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы вместе с интенсивностью отказов определяет безотказность объекта.
Основное уравнение радиолокации — формула, описывающая дальность действия радиолокатора, через расчет мощности радиосигналов и различных потерь. Для большинства пассивных радиолокаторов, являющихся моностатическими, мощность принимаемого сигнала уменьшается пропорционально 4-й степени расстояния, для активных локаторов мощность сигналов пропорциональна 2-й степени расстояния.

Многочлен Татта — многочлен от двух переменных, играющий большую роль в теории графов; определён для любого неориентированного графа и содержит информацию, насколько граф связен. Стандартное обозначение —  .
.
Минимально критичное остовное дерево во взвешенном неориентированном графе — это остовное дерево, в котором наиболее тяжёлое ребро весит как можно меньше. Критичное ребро — это самое тяжёлое ребро в стягивающем дереве. Стягивающее дерево является минимальным критичным остовным деревом, если граф не содержит стягивающего дерева с критичным ребром меньшего веса. Для ориентированного графа аналогичная задача известна как минимально критичное стягивающее ориентированное дерево.
Динамические стохастические модели общего равновесия — современные макроэкономические модели, параметры которых основаны на моделировании поведения экономических агентов на микроуровне, предусматривающие также моделирование различных стохастических «шоков».











































