
Гамма-функция — математическая функция. Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.

Джон Не́пер — шотландский математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц, астроном. 8-й лэрд Мерчистона из клана Непер.
Логарифмическое распределение в теории вероятностей — класс дискретных распределений. Логарифмическое распределение используется в различных приложениях, включая математическую генетику и физику.

Логнорма́льное распределе́ние (логарифмически-нормальное) в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то её логарифм имеет нормальное распределение.

Распределе́ние Ве́йбулла в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений.
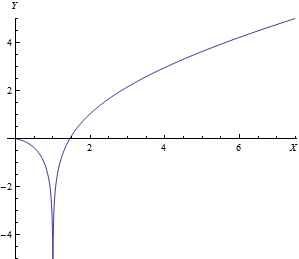
Интегральный логарифм — специальная функция, определяемая интегралом

Дискре́тное логарифми́рование (DLOG) — задача обращения функции  в некоторой конечной мультипликативной группе
в некоторой конечной мультипликативной группе  .
.
Расстояние Ку́льбака — Ле́йблера, РКЛ, информационное расхождение, различающая информация, информационный выигрыш, относительная энтропия — неотрицательнозначный функционал, являющийся несимметричной мерой удалённости друг от друга двух вероятностных распределений, определённых на общем пространстве элементарных событий. Часто применяется в теории информации и математической статистике.
В математике суперлогарифм — это одна из двух обратных функций тетрации.

Комплексный логарифм — аналитическая функция, получаемая распространением вещественного логарифма на всю комплексную плоскость. Существует несколько эквивалентных способов такого распространения. Данная функция имеет широкое применение в комплексном анализе. В отличие от вещественного случая, функция комплексного логарифма многозначна.
История логарифмов как алгебраического понятия прослеживается с античных времён. Идейным источником и стимулом применения логарифмов послужил тот факт, известный ещё во времена Архимеда, что при перемножении степеней с одинаковым основанием их показатели складываются:  .
.
Постоя́нная Хи́нчина — вещественная константа  , равная среднему геометрическому элементов разложения в цепную дробь любого из почти всех вещественных чисел.
, равная среднему геометрическому элементов разложения в цепную дробь любого из почти всех вещественных чисел.
Гипотеза Римана является одной из наиболее важных гипотез в математике. Гипотеза является утверждением о нулях дзета-функции Римана. Различные геометрические и арифметические объекты могут быть описаны так называемыми глобальными L-функциями, которые формально похожи на дзета-функцию Римана. Можно тогда задать тот же вопрос о корнях этих L-функций, что даёт различные обобщения гипотезы Римана. Многие математики верят в верность этих обобщений гипотезы Римана. Единственный случай, когда такая гипотеза была доказана, произошёл в алгебраическом поле функций.
Натуральный логарифм 2 в десятичной системе счисления равен приблизительно

Теоремы Мертенса — это три результата 1874 года, связанные с плотностью простых чисел, доказанные Францем Мертенсом. Название «теорема Мертенса» может относиться также к его теореме в анализе.





































