Неравенство Крафта — Макмиллана

В теории кодирования, неравенство Крафта — Макмиллана даёт необходимое и достаточное условие существования разделимых и префиксных кодов, обладающих заданным набором длин кодовых слов.

Пусть заданы два произвольных конечных множества, которые называются, соответственно, кодируемым алфавитом и кодирующим алфавитом. Их элементы называются символами, а строки (последовательности конечной длины) символов — словами. Длина слова — это число символов, из которого оно состоит.

В качестве кодирующего алфавита часто рассматривается множество ${\displaystyle \{0,1\}}$ — так называемый двоичный или бинарный алфавит.

Схемой алфавитного кодирования (или просто (алфавитным) кодом) называется любое отображение символов кодируемого алфавита в слова кодирующего алфавита, которые называют кодовыми словами. Пользуясь схемой кодирования, каждому слову кодируемого алфавита можно сопоставить его код — конкатенацию кодовых слов, соответствующих каждому символу этого слова.

Код называется разделимым (или однозначно декодируемым), если никаким двум словам кодируемого алфавита не может быть сопоставлен один и тот же код.

Префиксным кодом называется алфавитный код, в котором ни одно из кодовых слов не является префиксом никакого другого кодового слова. Любой префиксный код является разделимым.

Теорема Макмиллана (1956).

Пусть заданы кодируемый и кодирующий алфавиты, состоящие из ${\displaystyle n}$ и ${\displaystyle d}$ символов, соответственно, и заданы желаемые длины кодовых слов: ${\displaystyle \ell _{1},\ell _{2},\ldots ,\ell _{n}}$. Тогда необходимым и достаточным условием существования разделимого и префиксного кодов, обладающих заданным набором длин кодовых слов, является выполнение неравенства:

${\displaystyle \sum _{i=1}^{n}d^{\,-\ell _{i}}\leqslant 1.}$

Это неравенство и известно под названием неравенства Крафта — Макмиллана. Впервые оно было выведено Леоном Крафтом в своей магистерской дипломной работе в 1949 году^[1], однако он рассматривал только префиксные коды, поэтому при обсуждении префиксных кодов это неравенство часто называют просто неравенством Крафта. В 1956 году Броквэй Макмиллан доказал необходимость и достаточность этого неравенства для более общего класса кодов — разделимых кодов.^[2]

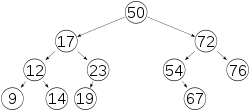
Любое укоренённое двоичное дерево можно рассматривать как графическое описание префиксного кода над двоичным алфавитом: символы кодируемого алфавита соответствуют листьям дерева, а путь в дереве от корня до листа задаёт его код (путь состоит из последовательности движений «влево» и «вправо», которые соответствуют символам 0 и 1).

Для таких деревьев неравенство Крафта — Макмиллана утверждает, что:

${\displaystyle \sum _{x\in {\mathcal {L}}}2^{-\mathrm {depth} (x)}\leqslant 1,}$

где ${\displaystyle {\mathcal {L}}}$ — множество листьев дерева, а ${\displaystyle \mathrm {depth} (x)}$ — глубина листа ${\displaystyle x}$, число рёбер на пути от корня до ${\displaystyle x}$.

Для дерева на рисунке справа имеем:

${\displaystyle {\frac {1}{4}}+4\left({\frac {1}{8}}\right)={\frac {3}{4}}\leqslant 1.}$

• Гашков, С. Б. Системы счисления и их применение. — М.: МЦНМО, 2004. — 52 с. — ISBN 5-94057-146-8.
• Cover, T. M., Thomas, J. A. Elements of information theory. — 2006. — P. 116. — ISBN 0-471-24195-4.

• Kraft’s inequality (NIST) Архивная копия от 27 января 2009 на Wayback Machine
• http://www.codingtheory.gorodok.net/seminars/seminar%2010.pdf Архивная копия от 5 марта 2016 на Wayback Machine