Фундамента́льная гру́ппа — одна из простейших конструкций в алгебраической топологии. Сопоставляется группа всякому связному топологическому пространству. Для подмножеств плоскости эта группа измеряет количество «дырок». Наличие «дырки» определяется невозможностью непрерывно продеформировать (стянуть) некоторую замкнутую кривую в точку.
Алгебраи́ческая тополо́гия — раздел топологии, изучающий топологические пространства путём сопоставления им алгебраических объектов, а также поведение этих объектов под действием различных топологических операций.
Топологи́ческое простра́нство — множество, для элементов которого определено, какие из них близки друг к другу. Является центральным понятием общей топологии.
В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глоссария.
Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Компа́ктное простра́нство — определённый тип топологических пространств, обобщающий свойства ограниченности и замкнутости в евклидовых пространствах на произвольные топологические пространства.
Разбиение единицы — конструкция, используемая в топологии для удобства работы с многообразием как с множеством карт.
Прямое произведение — множество, элементами которого являются все возможные упорядоченные пары элементов заданных двух непустых исходных множеств. Предполагается, что впервые «декартово» произведение двух множеств ввёл Георг Кантор.

Теорема Хелли — классический результат комбинаторной геометрии и выпуклого анализа. Теорема даёт условие на семейство выпуклых множеств, гарантирующее то, что это семейство имеет непустое пересечение.
Леммой Гейне — Бореля называется следующий факт, играющий фундаментальную роль в анализе:
- Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также покрывающую этот отрезок.
Размерность Хаусдорфа, или хаусдорфова размерность — естественный способ определить размерность подмножества в метрическом пространстве. Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой — единице, размерность гладкой поверхности — двум и размерность множества ненулевого объёма — трём. Для более сложных (фрактальных) множеств размерность Хаусдорфа может не быть целым числом.
Теорема Алекса́ндера о предбазе — теорема общей топологии, устанавливающая критерий компактности топологического пространства.
Произведение топологических пространств — это топологическое пространство, полученное, как множество, декартовым произведением исходных топологических пространств, и снабжённое естественной топологией, называемой топологией произведения или тихоновской топологией. Слово «естественная» здесь употребляется в смысле теории категорий и означает, что эта топология удовлетворяет некоторому универсальному свойству.
CW-комплекс — тип топологического пространства с дополнительной структурой, введённый Уайтхедом для удовлетворения нужд теории гомотопий. В литературе на русском языке употребляются также названия клеточное пространство, клеточное разбиение и клеточный комплекс. Класс клеточных комплексов является более широким, чем класс симплициальных комплексов, но в то же время сохраняет комбинаторную природу, которая позволяет производить эффективные вычисления.
Когомологии Александрова — Чеха — теория когомологий, основанная на свойствах открытых покрытий топологического пространства. Такие когомологии оказываются удобными при изучении патологических пространств.
Теорема Зейферта — ван Кампена выражает фундаментальную группу топологического пространства через фундаментальные группы двух открытых подмножеств, покрывающих пространство.
Когомологии пучков — это результат использования гомологической алгебры для исследования глобальных сечений пучков. Грубо говоря, когомологии пучков описывают препятствия к глобальному решению геометрической проблемы, когда она может быть решена локально.
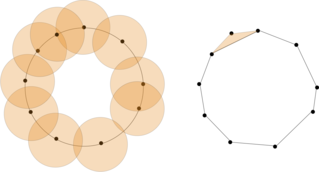
Комплекс Чеха — абстрактный симплициальный комплекс, построенный по облаку точек в любом метрическом пространстве, предназначенный для получения топологической информации об облаке точек или распределении, при помощи которого выбираются точки. Широко используется в топологическом анализе данных.

















