Лине́йная а́лгебра — раздел алгебры, изучающий математические объекты линейной природы: векторные пространства, линейные отображения, системы линейных уравнений. Среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно также считаются составными частями линейной алгебры. Такие объекты как квадратичные и билинейные формы, тензоры и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.

Ве́кторное простра́нство — математическая структура, представляющая собой набор элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр. Эти операции подчинены восьми аксиомам. Скаляры могут быть элементами вещественного, комплексного или любого другого поля чисел. Частным случаем подобного пространства является обычное трёхмерное евклидово пространство, векторы которого используются, к примеру, для представления физических сил. При этом вектор как элемент векторного пространства не обязательно должен быть задан в виде направленного отрезка. Обобщение понятия «вектор» до элемента векторного пространства любой природы не только не вызывает смешения терминов, но и позволяет уяснить или даже предвидеть ряд результатов, справедливых для пространств произвольной природы.

В математике, если заданы две группы (G, ∗) и (H, •), гомоморфизм групп из (G, ∗) в (H, •) — это функция h : G → H, такая, что для всех u и v из G выполняется


Те́нзор — применяемый в математике и физике математический объект линейной алгебры, заданный на векторном пространстве конечной размерности. В физике в качестве векторного пространства обычно выступает физическое трёхмерное пространство или четырёхмерное пространство-время, а компонентами тензора являются координаты (проекции) взаимосвязанных физических величин. Использование тензоров в физике позволяет глубже понять физические законы и уравнения, упростить их запись за счёт сведения многих связанных физических величин в один тензор, а также записывать уравнения в форме, не зависящей от выбранной системы отсчёта.

Симметрическая группа — группа всех перестановок заданного множества  относительно операции композиции.
относительно операции композиции.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задаёт размер матрицы. Матрицу можно также представить в виде функции двух дискретных аргументов. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Ба́зис — упорядоченный набор векторов в векторном пространстве или модуле, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора. Векторы базиса называются базисными векторами.
Спино́р — специальное обобщение понятия вектора, применяемое для лучшего описания группы вращений евклидова или псевдоевклидова пространства.
След — отображение элементов конечного расширения поля  в исходное поле K, определяемое следующим образом:
в исходное поле K, определяемое следующим образом:
Теорема Дирихле о единицах — теорема алгебраической теории чисел, описывающая ранг подгруппы обратимых элементов кольца алгебраических целых  числового поля
числового поля  .
.
Ба́наховой алгеброй над комплексным или действительным полем называется ассоциативная алгебра, являющаяся при этом банаховым пространством. При этом умножение в ней должно быть согласовано с нормой:
 .
.
Бикватернионы — комплексификация (расширение) обычных (вещественных) кватернионов.
Алгебраическое числовое поле, поле алгебраических чисел — это конечное расширение поля рациональных чисел  . Таким образом, числовое поле — это поле, содержащее
. Таким образом, числовое поле — это поле, содержащее  и являющееся конечномерным векторным пространством над ним. При этом некоторые авторы называют числовым полем любое подполе комплексных чисел — например, М. М. Постников в «Теории Галуа».
и являющееся конечномерным векторным пространством над ним. При этом некоторые авторы называют числовым полем любое подполе комплексных чисел — например, М. М. Постников в «Теории Галуа».

Симметрия встречается не только в геометрии, но и в других областях математики. Симметрия является видом инвариантности, свойством неизменности при некоторых преобразованиях.
В математике проективная специальная линейная группа PSL(2, 7) — это конечная простая группа, имеющая важные приложения в алгебре, геометрии и теории чисел. Она является группой автоморфизмов квартики Клейна, а также группой симметрии плоскости Фано. Имея 168 элементов, PSL(2, 7) является второй по величине из самых маленьких неабелевых простых групп.

Группа Лоренца является группой Ли симметрий пространства-времени в специальной теории относительности. Эта группа может быть реализована как набор матриц, линейных преобразований или унитарных операторов на некотором гильбертовом пространстве. Группа имеет различные представления. В любой релятивистски инвариантной физической теории эти представления как-то должны быть отражены. Сама физика должна быть сделана на их основе. Более того, специальная теория относительности вместе с квантовой механикой являются двумя физическими теориями, которые тщательно проверены и объединение этих двух теорий сводится к изучению бесконечномерных унитарных представлений группы Лоренца. Это имеет как историческую важность в основном течении в теоретической физике, так и связи с более спекулятивными теориями настоящего времени.
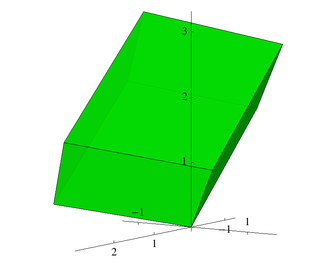
Дискриминант алгебраического числового поля — это числовой инвариант, который, грубо говоря, измеряет размер алгебраического числового поля. Более конкретно, он пропорционален квадрату объёма фундаментальной области кольца целых чисел и он определяет, какие простые числа разветвляются.
Симметрии в квантовой механике — преобразования пространства-времени и частиц, которые оставляют неизменными уравнения квантовой механики. Рассматриваются во многих разделах квантовой механики, которые включают релятивистскую квантовую механику, квантовую теорию поля, стандартную модель и физику конденсированного состояния. В целом, симметрия в физике, законы инвариантности и сохранения являются основополагающими ограничениями для формулирования физических теорий и моделей. На практике это мощные методы решения задач и прогнозирования того, что может случиться. Хотя законы сохранения не всегда дают конечное решение проблемы, но они формируют правильные ограничения и наметки к решению множества задач.

В математике структурные константы или структурные коэффициенты алгебры над полем используются для явного указания произведения двух базисных векторов в алгебре в качестве линейной комбинации. Учитывая структурные константы, результирующее произведение является билинейным и может быть однозначно расширено на все векторы в векторном пространстве, таким образом, однозначно определяя произведение для алгебры.






![{\displaystyle N_{K}^{E}(\alpha )=\alpha ^{[E:K]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d89d204b71b5868535f790c9c8c999361490596)
































