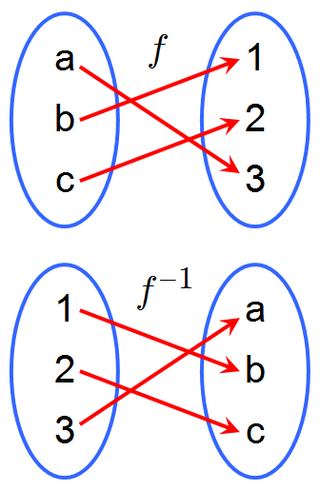
Бие́кция — отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют также взаимно однозначным отображением (соответствием).

Фу́нкция — соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого.
Тригономе́трия — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии для вычисления одних элементов треугольника по данным о других его элементах.
Непрерывная функция — функция, которая меняется без мгновенных «скачков», то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.

Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.

Фу́нкция Гри́на — функция, используемая для решения линейных неоднородных дифференциальных уравнений с граничными условиями . Названа в честь английского математика Джорджа Грина, который первым развил соответствующую теорию в 1830-е годы.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
- арксинус
- арккосинус
- арктангенс
- арккотангенс
- арксеканс
- арккосеканс
Пучок — структура, используемая для установления отношений между локальными и глобальными свойствами или характеристиками некоторого математического объекта. Пучки играют значительную роль в топологии, дифференциальной геометрии и алгебраической геометрии, но также применяются в теории чисел, анализе и теории категорий.
Числова́я фу́нкция — функция, которая действует из одного числового пространства (множества) в другое числовое пространство (множество). Числовые множества — это множества натуральных, целых, рациональных, вещественных и комплексных чисел вместе с определёнными для соответствующих множеств алгебраическими операциями. Для всех перечисленных числовых множеств, кроме комплексных чисел, определено также отношение линейного порядка, позволяющее сравнивать числа по величине. Числовые пространства — это числовые множества вместе с функцией расстояния, заданной на соответствующем множестве.
Ба́наховой алгеброй над комплексным или действительным полем называется ассоциативная алгебра, являющаяся при этом банаховым пространством. При этом умножение в ней должно быть согласовано с нормой:
 .
.
Теорема об обратной функции даёт достаточные условия для существования обратной функции в окрестности точки через производные от самой функции.