Обучающий, проверочный и тестовый наборы данных

Перейти к навигацииПерейти к поиску

В машинном обучении, общей задачей является изучение и построение алгоритмов, которые могут быть обучаемы и делать прогнозы с помощью данных.[1] Такие алгоритмы работают, делая прогнозы или решения основываясь на данных,[2] с помощью построения математической модели основанной на входных данных. Эти входные данные используемые для построения модели обычно поделены на несколько наборов данных. В частности, три набора данных обычно используются на разных этапах построения модели: обучающий, проверочный и тестовый.

Изначально модель тренируются с помощью обучающего набора данных (training dataset),[3], который является набором примеров используемых для настройки параметров (например, веса соединений между нейронами в искусственных нейронных сетях) модели.[4] Модель (например, наивный байесовский классификатор) обучается на обучающем наборе данных, (см. обучение с учителем) например, используя методы оптимизации, такие как градиентный спуск или стохастический градиентный спуск. На практике обучающий набор данных часто состоит из пар входного вектора (или скаляра) и соответствующего выходного вектора (или скаляра), где выходное значение обычно обозначается как цель (или метка). Модель обучается с помощью обучающего набора данных и производит результат, который затем сравнивается с меткой, для каждого входного вектора в обучающем наборе данных. Основываясь на результате сравнения и характере используемого алгоритма машинного обучения, параметры модели подстраиваются соответствующим образом. Настройка модели может включать процессы отбора признаков и оценивания параметров.

Далее, обученная модель используется для прогнозирования ответов для наблюдения с помощью второго набора данных, называемого проверочный набор данных (validation dataset).[3] Проверочный набор данных предоставляет непредвзятую оценку модели, обученной с помощью обучающего набора данных, в то же время подстраивая гиперпараметры модели[5] (например, число скрытых слоев и ширину слоев в нейронной сети)[4]). Проверочные наборы данных могут быть использованы для регуляризации обучения с помощью метода ранней остановки (остановки обучения, в тот момент, когда ошибка на проверочном наборе данных начинает увеличиваться, так как это является признаком переобучения на обучающем наборе данных).[6]

Эта простая процедура осложняется на практике тем фактом, что ошибка проверочного набора данных может колебаться во время обучения, создавая несколько локальных минимумов. Это осложнение привело к созданию множества специальных правил для определения ситуаций, в которых началось переобучение.[6]

Наконец, тестовый набор данных (test dataset) — это набор данных, используемый для непредвзятой оценки окончательной модели, настроенной с помощью обучающего набора данных.[5] Если данные в тестовом наборе данных никогда не были использованы в обучении (например, в перекрёстной проверке), тестовый набор данных также называется удержанным набором данных (holdout dataset). В некоторой литературе термин «проверочный набор» иногда используется вместо «тестового набора» (например, если изначальный набор данных был разделен только на два набора, тестовый набор может называться проверочным набором).[5]

Принятие решения о размерах и стратегиях разделения набора данных на обучающий, тестовый и проверочный наборы сильно зависит от проблемы и имеющихся данных.[7]

Обучающий набор данных

Обучающий набор данных — это набор данных экземпляров, используемых во время обучающего процесса и используемых для настройки параметров (например, веса в классификаторе).[8][9]

В задачах классификации, алгоритм обучения с учителем изучает обучающий набор данных для обнаружения, или обучения, оптимальной комбинации переменных, для генерирования хорошей прогнозной модели.[10] Главной целью является создание обученной (настроенной) модели, которая хорошо делает общие выводы на новых, не использованных данных.[11] Настроенная модель оценивается с помощью «новых» примеров из удержанных наборов данных (проверочного и тестового) для оценки аккуратности модели для классификации новых данных.[5] Для уменьшения риска появления проблем, таких как переобучение, экземпляры в проверочном и тестовом наборе данных не должны быть использованы для обучения модели.[5]

Большинство подходов, предназначенных для поиска эмпирических отношений с использованием обучающих данных имеют тенденцию переобучаться, это означает то, что они могут находить и использовать явные отношения в обучающих данных, которые не применимы для всей генеральной совокупности.

Проверочный набор данных

Проверочный набор данных — это набор данных примеров, используемых для настройки гиперпараметров (например, архитектура классификатора). Он иногда также называется набором разработки (development set) или «dev set».[12] Примером гиперпараметров искусственной нейронной сети является число скрытых узлов в каждом слое.[8][9] Этот набор, также как и тестовый набор (как упоминается ниже) должен иметь такое же распределение вероятности, как и обучающий набор.

Для избежания переобучения, необходимо иметь проверочный набор данных в дополнение к обучающему и тестовому наборам данных. Например, если осуществляется поиск наиболее подходящего классификатора для задачи, обучающий набор данных используется для обучения различных классификаторов-кандидатов, в то время как, проверочный набор используется для сравнения их производительности и выбора наиболее подходящего, наконец, обучающий набор данных используется для получения характеристик производительности таких как точность, чувствительность, специфичность, F-мера, и так далее. Проверочный набор данных работает как гибрид: его обучающие данные используются для тестирования, но ни как для первоначального обучения, и ни как часть, финального тестирования.

Основной процесс, использующий проверочный набор данных для выбора модели (как часть обучающего набора данных, проверочного набора данных, и тестового набора данных) состоит в следующем:[9][13]

Так как нашей целью является поиск сети обладающей лучшей производительностью на новых данных, самый простой подход для сравнения различных сетей — это оценка функции ошибки с использованием данных, которые независимы от данных, используемых для обучения. Различные сети обучаются с помощью минимизации соответствующей функции ошибки, определенной в соответствии с обучающим набором данных. Производительность сетей затем сравнивается с помощью оценки функции ошибки, с использованием независимого проверочного набора; сеть, имеющая самую маленькую ошибку в соответствии с проверочным набором, выбирается в качестве наиболее подходящей. Это подход называется методом удержания hold out. Так как эта процедура может сама приводить к некоторому переобучению с помощью проверочного набора, производительность выбранной сети должна быть подтверждена с помощью третьего независимого набора данных, называемого тестовым набором

Этот процесс находит применение в ранней остановке, когда модели-кандидаты являются последовательными итерациями одной и той же сети, и обучение останавливается, когда ошибка на проверочном наборе начинает расти, и в качестве финальной модели выбирается предыдущая модель (с минимальной ошибкой).

Тестовый набор данных

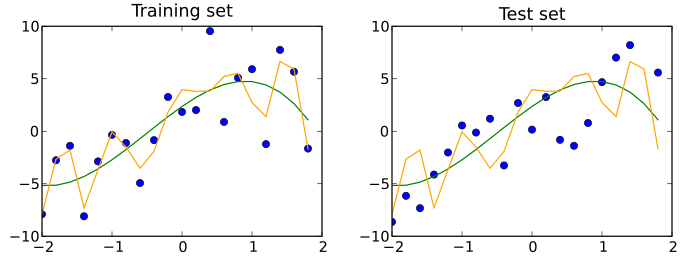
Тестовый набор данных — это набор данных, который независим от обучающего набора данных, но который соответствует такому же распределению вероятностей, как и обучающий набор данных. Если модель, подходящая для обучающего набора данных, также хорошо подходит для тестового набора данных, то произошло минимальное переобучение (смотри изображение ниже). Лучшее соответствие модели обучающему набору данных, в противовес тестовому набору данных обычно указывает на её переобучение.

Таким образом, тестовый набор является набором примеров, используемых только для оценки производительности (например, обобщения) полностью определенного классификатора.[8][9] Для произведения этой оценки окончательная модель используется для прогнозирования классификация на экземплярах тестового набора. Эти прогнозирования сравниваются с экземплярами настоящей классификации для оценки аккуратности модели.[10]

В ситуациях, когда используются проверочный и тестовый наборы данных, тестовый набор данных обычно используется для оценки окончательной модели, которая выбирается во время процесса тестирования. В случае, когда первоначальный набор данных делится на два набора (обучающий и тестовый набор данных), тестовый набор данных может оценить модель только один раз (например, в методе удержания[англ.]).[14] Следует заметить, что некоторые ресурсы выступают против использования данного метода.[11] Как бы там ни было, при использовании методов, например таких как, перекрёстная проверка, использование двух наборов данных может быть достаточно и эффективно, так как результаты усредняются после повторных этапов обучения и тестирования модели для уменьшения предвзятости и непостоянства.[5][11]

Обучающий набор (слева) и тестовый набор (справа) из той же генеральной совокупности показаны голубыми точками. Две модели прогнозирования соответствуют обучающим данным. Обе обученные модели изображены вместе с обучающим и тестовым наборами данных. В обучающем наборе, MSE обучения показана оранжевым цветом и равна 4, в то время как MSE для обучения показана зеленым и равна 9. В тестовом наборе, MSE для обучения показана оранжевым и равна 15, а MSE обучения показана зеленым равна 13. Оранжевая кривая слишком сильно соответствует обучающим данным, так как её среднеквадратическая ошибка увеличивается почти в 4 раза при сравнении тестового и обучающего набора данных. Зеленая кривая соответствует обучающим данным намного меньше, так как её MSE увеличивается менее чем в два раза.

Путаница в терминологии

Тестирование — это попытка узнать что-то попробовав это («Для доказательства; доказать истину, подлинность или качество путем эксперимента» в соответствии с Совместным международным словарем английского языка, а валидация — это подтверждение того, что что-то корректно («Подтвердить;» Совместный международный словарь английского языка). Рассматривая с этой точки зрения, самое распространенное использование терминов тестовый набор и проверочный набор — это то, которое приведено выше. Однако, как в производственных, так и в научных кругах, эти термины иногда взаимозаменяемы, с учётом того, что внутренний процесс — это тестирование различных моделей для улучшения (тестовый набор как набор разработчика) и окончательная модель, это та, которая должна быть проверена перед промышленным использованием с невидимыми до этого данными (проверочный набор). "Литература машинного обучения часто переворачивает значение 'проверочного' и 'тестового' наборов. Это самый яркий пример терминологической путаницы, который пронизывает исследования искусственного интеллекта.[15] Тем не менее, важный концепт о котором необходимо помнить заключается в том, что финальный набор, называющийся тестовым или проверочным, должен быть использован только в окончательном эксперименте.

Перекрёстная проверка

Для того чтобы получить более стабильные результаты и использовать все значимые данные для обучения, набор данных может быть повторно разделен на несколько обучающих и проверочных наборов данных. Этот метод известен как перекрёстная проверка. Для подтверждения производительности модели обычно используются дополнительные тестовые наборы данных, удерживаемые для использования в перекрёстной проверке.

См. также

Примечания

  1. ↑ Ron Kohavi; Foster Provost (1998). "Glossary of terms". Machine Learning. 30: 271—274. doi:10.1023/A:1007411609915. Архивировано 11 ноября 2019. Дата обращения: 15 февраля 2023.
  2. ↑ Bishop, Christopher M. Pattern Recognition and Machine Learning. — New York : Springer, 2006. — P. vii. — «Pattern recognition has its origins in engineering, whereas machine learning grew out of computer science. However, these activities can be viewed as two facets of the same field, and together they have undergone substantial development over the past ten years.». — ISBN 0-387-31073-8.
  3. ↑ 1 2 James, Gareth. An Introduction to Statistical Learning: with Applications in R. — Springer, 2013. — P. 176. — ISBN 978-1461471370. Архивная копия от 23 июня 2019 на Wayback Machine
  4. ↑ 1 2 Ripley, Brian. Pattern Recognition and Neural Networks. — Cambridge University Press, 1996. — P. 354. — ISBN 978-0521717700.
  5. ↑ 1 2 3 4 5 6 Brownlee, Jason What is the Difference Between Test and Validation Datasets? (13 июля 2017). Дата обращения: 12 октября 2017. Архивировано 10 декабря 2019 года.
  6. ↑ 1 2 Prechelt, Lutz. Early Stopping — But When? // Neural Networks: Tricks of the Trade / Lutz Prechelt, Geneviève B. Orr. — Springer Berlin Heidelberg, 2012-01-01. — P. 53–67. — ISBN 978-3-642-35289-8. — doi:10.1007/978-3-642-35289-8_5.
  7. ↑ Machine learning - Is there a rule-of-thumb for how to divide a dataset into training and validation sets? Stack Overflow. Дата обращения: 12 августа 2021. Архивировано 12 августа 2021 года.
  8. ↑ 1 2 3 Ripley, B.D. (1996) Pattern Recognition and Neural Networks, Cambridge: Cambridge University Press, p. 354
  9. ↑ 1 2 3 4 «Subject: What are the population, sample, training set, design set, validation set, and test set? Архивная копия от 10 марта 2021 на Wayback Machine», Neural Network FAQ, part 1 of 7: Introduction Архивная копия от 10 марта 2021 на Wayback Machine (txt), comp.ai.neural-nets, Sarle, W.S., ed. (1997, last modified 2002-05-17)
  10. ↑ 1 2 Larose, D. T. Discovering knowledge in data : an introduction to data mining / D. T. Larose, C. D. Larose. — Wiley, 2014. — ISBN 978-0-470-90874-7. — doi:10.1002/9781118874059.
  11. ↑ 1 2 3 Xu, Yun; Goodacre, Royston (2018). "On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning". Journal of Analysis and Testing. 2 (3). Springer Science and Business Media LLC: 249—262. doi:10.1007/s41664-018-0068-2. ISSN 2096-241X. PMC 6373628. PMID 30842888.
  12. ↑ Deep Learning (англ.). Coursera. Дата обращения: 18 мая 2021. Архивировано 16 мая 2021 года.
  13. ↑ Bishop, C.M. (1995), Neural Networks for Pattern Recognition, Oxford: Oxford University Press, p. 372
  14. ↑ Kohavi, Ron (2001-03-03). "A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection". 14. {{cite journal}}: Cite journal требует |journal= ()
  15. ↑ Ripley, Brian D. Pattern recognition and neural networks. — Cambridge Univ. Press, 2009. — P. Glossary. — ISBN 9780521717700.