Однородная мозаика
Однородная мозаика — вершинно транзитивная мозаика на плоскости с правильными многоугольными гранями.
Однородная мозаика может существовать как на евклидовой плоскости, так и на гиперболической плоскости. Однородные мозаики связаны с конечными однородными многогранниками, которые можно считать однородными замощениями сферы.
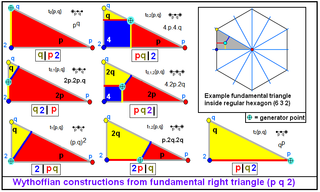
Большинство однородных мозаик могут быть получены построением Витхоффа с помощью симметрии, начиная с одной генерирующей точки внутри фундаментальной области. Группа симметрии на плоскости имеет многоугольную фундаментальную область и может быть представлена порядком зеркал в последовательности вершин.
Треугольная фундаментальная область имеет порядки зеркал (p q r), а прямоугольная треугольная область — (p q 2), где p, q, r — целые числа, большие единицы. Треугольник может быть сферическим треугольником, евклидовым треугольником или треугольником на гиперболической плоскости, что зависит от значений p, q и r.
Существует несколько символических схем для именования полученных фигур, начиная с модифицированного символа Шлефли для фундаментальной области в виде прямоугольного треугольника (p q 2) → {p, q}. Диаграмма Коксетера — Дынкина является графом с помеченными значениями p, q, r рёбрами. Если r = 2, граф линеен, поскольку узлы порядка 2 не образуют отражений. Символ Витхоффа[англ.] использует 3 целых числа с разделительной вертикальной чертой между ними (|). Если генерирующая точка не находится на зеркале, символ вершины, противоположной зеркалу, помещается до вертикальной черты.
Наконец, мозаики можно описать с помощью их вершинной конфигурации, т.е. последовательности многоугольников вокруг каждой вершины.
Все однородные мозаики можно построить с помощью различных операций, применённых к правильным мозаикам. Имена этим операциям дал американский математик Норман Джонсон, это truncation (усечение, отрезание вершин), rectification (полное усечение, отрезание вершин до полного исчезновения исходных рёбер) и cantellation (скашивание, срезание рёбер). Omnitruncation (всеусечение[англ.]) — это операция, комбинирующая усечение и скашивание. Snubbing (отрезание носов) — это операция альтернированного усечения всеусечённых форм. (См. Операторы построения Витхоффа для подробного объяснения операций.)
Группы Коксетера
Группы Коксетера на плоскости определяют построение Витхоффа и могут быть представлены диаграммами Коксетера — Дынкина:
Для групп с целым числовым порядком:
| Орбифолдная симметрия[англ.] | Группа Коксетера | Диаграмма Коксетера | Примечания | ||
|---|---|---|---|---|---|
| Компактные | |||||
| *333 | (3 3 3) | [3[3]] | 3 зеркальные формы, 1 плосконосая | ||
| *442 | (4 4 2) | [4,4] | 5 зеркальных форм, 1 плосконосая | ||
| *632 | (6 3 2) | [6,3] | 7 зеркальных форм, 1 плосконосая | ||
| *2222 | (∞ 2 ∞ 2) | × | [∞,2,∞] | 3 зеркальные формы, 1 плосконосая | |
| Некомпактные (бордюр) | |||||
| *∞∞ | (∞) | [∞] | |||
| *22∞ | (2 2 ∞) | × | [∞,2] | 2 зеркальные формы, 1 плосконосая | |
| Орбифолдная симметрия[англ.] | Группа Коксетера | Диаграмма Коксетера | Примечания | |
|---|---|---|---|---|
| Компактные | ||||
| *pq2 | (p q 2) | [p,q] | 2(p+q) < pq | |
| *pqr | (p q r) | [(p,q,r)] | pq+pr+qr < pqr | |
| Паракомпактные | ||||
| *∞p2 | (p ∞ 2) | [p,∞] | p>=3 | |
| *∞pq | (p q ∞) | [(p,q,∞)] | p,q>=3, p+q>6 | |
| *∞∞p | (p ∞ ∞) | [(p,∞,∞)] | p>=3 | |
| *∞∞∞ | (∞ ∞ ∞) | [(∞,∞,∞)] | ||
Однородные мозаики на евклидовой плоскости
Имеются группы симметрии на евклидовой плоскости, получающиеся из фундаментальных треугольников (4 4 2), (6 3 2) и (3 3 3). Каждая из них представляется набором прямых (зеркал), делящих плоскость на фундаментальные треугольники.
Эти группы симметрии создают 3 правильных мозаики и 7 полуправильных. Число полуправильных мозаик повторяется при различных конструкциях симметрии.
Призматическая группа симметрии, представленная символом (2 2 2 2), задаётся двумя наборами параллельных зеркал, что, в общем случае, может иметь прямоугольную фундаментальную область. Группа не образует новых мозаик.
Далее — призматическая группа симметрии, представленная символом (∞ 2 2), имеет бесконечную фундаментальную область. Группа даёт две однородные мозаики, бесконечноугольную призму[англ.] и бесконечноугольную антипризму[англ.].
При совмещении конечных граней этих двух призматических мозаик получим невитхоффову однородную мозаику на плоскости. Она называется изокурносым треугольным паркетом[англ.] и состоит из поочерёдных слоёв квадратов и треугольников.
Прямоугольный фундаментальный треугольник (p q 2)
| (p q 2) | Фунд. треугольники | Родитель | Усеченная | Полностью усечённая | Биусечённая | Полностью биусечённая (двойственная) | Скошенная | Всеусечённая | Плосконосая |
|---|---|---|---|---|---|---|---|---|---|
| Символ Витхоффа | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Символ Шлефли | t{p,q} | t{p,q} | r{p,q} | 2t{p,q}=t{q,p} | 2r{p,q}={q,p} | rr{p,q} | tr{p,q} | sr{p,q} | |
| Диаграмма Коксетера | |||||||||
| Вершинная фигура | pq | q.2p.2p | (p.q)2 | p. 2q.2q | qp | p. 4.q.4 | 4.2p.2q | 3.3.p. 3.q | |
| Квадратная мозаика (4 4 2) |  |  {4,4} |  4.8.8 |  4.4.4.4 |  4.8.8 |  {4,4} |  4.4.4.4 |  4.8.8 |  3.3.4.3.4 |
| Шестиугольная мозаика (6 3 2) |  |  {6,3} |  3.12.12[англ.] |  3.6.3.6 |  6.6.6 |  {3,6} |  3.4.6.4[англ.] |  4.6.12[англ.] |  3.3.3.3.6 |
Фундаментальные треугольники общего вида (p q r)
| символ Витхоффа (p q r) | Фунд. треугольники | q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Диаграмма Коксетера | |||||||||
| Вершинная конфигурация | (p.q)r | r.2p.q.2p | (p.r)q | q.2r.p. 2r | (q.r)p | q.2r.p. 2r | r.2q.p. 2q | 3.r.3.q.3.p | |
| Треугольная (3 3 3) |  |  (3.3)3 |  3.6.3.6 |  (3.3)3 |  3.6.3.6 |  (3.3)3 |  3.6.3.6 |  6.6.6 |  3.3.3.3.3.3 |
Несимплициальные фундаментальные области
Единственной возможной фундаментальной областью в евклидовом пространстве, не являющейся симплексом, является прямоугольник (∞ 2 ∞ 2) с диаграммой Коксетера ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Из этой области становятся получаются только квадратные паркеты.
. Из этой области становятся получаются только квадратные паркеты.
Однородные мозаики на гиперболической плоскости
Существует бесконечно много однородных мозаик из выпуклых правильных многоугольников на гиперболической плоскости, каждая из которых основана на различных группах зеркальной симметрии (p q r).
Примеры, показанные здесь, даны в проекции на диск Пуанкаре.
Диаграммы Коксетера — Дынкина даны в линейной форме, хотя, на самом деле, это треугольники, в которых конечный сегмент r соединён с первым узлом.
Кроме того, на гиперболической плоскости существуют четырёхугольные фундаментальные области, начиная с (2 2 2 3), которые могут образовать новые формы. Также существуют фундаментальные области с вершинами на бесконечности, такие как (∞ 2 3).
Прямоугольные фундаментальные треугольники (p q 2)
| (p q 2) | Фунд. треугольники | Родитель | Усечённая | Полностью усечённая | Биусечённая | Полностью биусечённая (двойственная) | Скошенная | Всеусечённая | Плосконосая |
|---|---|---|---|---|---|---|---|---|---|
| Символ Витхоффа | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Символ Шлефли | t{p,q} | t{p,q} | r{p,q} | 2t{p,q}=t{q,p} | 2r{p,q}={q,p} | rr{p,q} | tr{p,q} | sr{p,q} | |
| Диаграмма Коксетера — Дынкина | |||||||||
| Вершинная фигура | pq | (q.2p.2p) | (p.q.p.q) | (p. 2q.2q) | qp | (p. 4.q.4) | (4.2p.2q) | (3.3.p. 3.q) | |
| (Гиперболическая плоскость) (5 4 2) |  V4.8.10 |  {5,4} |  4.10.10 |  4.5.4.5 | 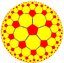 5.8.8 |  {4,5} |  4.4.5.4 |  4.8.10 |  3.3.4.3.5 |
| (Гиперболическая плоскость) (5 5 2) |  V4.10.10 |  {5,5} | 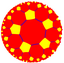 5.10.10 |  5.5.5.5 | 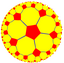 5.10.10 |  {5,5} |  5.4.5.4 |  4.10.10 |  3.3.5.3.5 |
| (Гиперболическая плоскость) (7 3 2) |  V4.6.14 |  {7,3} |  3.14.14 |  3.7.3.7[англ.] |  7.6.6 |  {3,7}[англ.] |  3.4.7.4 |  4.6.14[англ.] |  3.3.3.3.7 |
| (Гиперболическая плоскость) (8 3 2) |  V4.6.16 |  {8,3}][англ.] |  3.16.16 |  3.8.3.8[англ.] |  8.6.6 |  {3,8}[англ.] |  3.4.8.4 |  4.6.16[англ.] |  3.3.3.3.8 |
Фундаментальные треугольники (p q r) общего вида
| Символ Витхоффа (p q r) | Фундам. треугольники | q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Диаграмма Коксетера — Дынкина | |||||||||
| Вершинная фигура | (p.r)q | (r.2p.q.2p) | (p.q)r | (q.2r.p. 2r) | (q.r)p | (r.2q.p. 2q) | (2p.2q.2r) | (3.r.3.q.3.p) | |
| Гиперболические (4 3 3) | 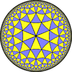 V6.6.8 |  (3.4)3 |  3.8.3.8 |  (3.4)3 |  3.6.4.6 |  (3.3)4 |  3.6.4.6 |  6.6.8 |  3.3.3.3.3.4 |
| Гиперболические (4 4 3) |  V6.8.8 |  (3.4)4 |  3.8.4.8 |  (4.4)3 |  3.6.4.6 |  (3.4)4 |  4.6.4.6 |  6.8.8 |  3.3.3.4.3.4 |
| Гиперболические (4 4 4) |  V8.8.8 |  (4.4)4 |  4.8.4.8 |  (4.4)4 |  4.8.4.8 |  (4.4)4 |  4.8.4.8 |  8.8.8 |  3.4.3.4.3.4 |
Расширенный список однородных мозаик
Существует несколько путей расширения списка однородных мозаик:
- Вершинные фигуры могут иметь вырожденные грани и оборачиваться вокруг вершины более одного раза.
- Можно включить мозаики со звёздчатыми многоугольниками.
- В качестве граней мозаик могут использоваться апейрогоны, {∞}.
- Может быть отброшено ограничение, что грани мозаики соприкасаются ребро-к-ребру, что даёт дополнительные мозаики, такие как пифагорова мозаика.
Треугольники групп симметрии с вырожденными гранями включают:
- (4/3 4/3 2) (6 3/2 2) (6/5 3 2) (6 6/5 3) (6 6 3/2)
Треугольники групп симметрии с бесконечностями включают:
- (4 4/3 ∞) (3/2 3 ∞) (6 6/5 ∞) (3 3/2 ∞)
Бранко Грюнбаум в книге 1987 года Tilings and patterns (Мозаики и узоры) в секции 12.3 приводит список 25 однородных мозаик, включающих 11 выпуклых и ещё 14, которые он называет мозаиками с впадинами. Среди последних включены первые две расширенные мозаики, указанные выше, мозаики со звёздчатыми многоугольными гранями и вершинными фигурами.
Гарольд Коксетер и др. в статье 1954 года 'Uniform polyhedra' (Однородные многогранники) в Таблице 8 Однородные замощения указывает первые три расширения и приводит список из 38 однородных мозаик.
Наконец, если считать мозаики с 2 бесконечноугольниками, можно насчитать, в общей сложности, 39 однородных мозаик.

7 новых мозаик с {∞} гранями с вершинными фигурами и символами Витхоффа[англ.]:
- ∞.∞ (две грани в виде полуплоскостей, бесконечный диэдр)
- 4.4.∞ — ∞ 2 | 2 (бесконечноугольная призма[англ.])
- 3.3.3.∞ — | 2 2 ∞ (бесконечноугольная антипризма[англ.])
- 4.∞.4/3.∞ — 4/3 4 | ∞ (альтернированный квадратный паркет)
- 3.∞.3.∞.3.∞ — 3/2 | 3 ∞ (альтернированный треугольный паркет)
- 6.∞.6/5.∞ — 6/5 6 | ∞ (альтернированная тришестиугольная мозаика, только с шестиугольниками)
- ∞.3.∞.3/2 — 3/2 3 | ∞ (альтернированная тришестиугольная мозаика, только с треугольниками)
Оставшийся список включает 21 мозаику с 7 {∞} гранями (бесконечноугольники). Если нарисовать мозаики как графы, останется только 14 уникальных мозаик, и первая идентична мозаике 3.4.6.4.

21 мозаик, сгруппированных по общим графам с указанием вершинной фигуры и символа Витхоффа:
| Тип | Вершинная конфигурация | Символ Витхоффа |
|---|---|---|
| 1 | 3/2.12.6.12 | 3/2 6 | 6 |
| 4.12.4/3.12/11 | 2 6 (3/2 3) | | |
| 2 | 8/3.4.8/3.∞ | 4 ∞ | 4/3 |
| 8/3.8.8/5.8/7 | 4/3 4 (2 ∞) | | |
| 8.4/3.8.∞ | 4/3 ∞ | 4 | |
| 3 | 12/5.6.12/5.∞ | 6 ∞ | 6/5 |
| 12/5.12.12/7.12/11 | 6/5 6 (3 ∞) | | |
| 12.6/5.12.∞ | 6/5 ∞ | 6 | |
| 4 | 12/5.3.12/5.6/5 | 3 6 | 6/5 |
| 12/5.4.12/7.4/3 | 2 6/5 (3/2 3) | | |
| 4.3/2.4.6/5 | 3/2 6 | 2 | |
| 5 | 8.8/3.∞ | 4/3 4 ∞ | |
| 6 | 12.12/5.∞ | 6/5 6 ∞ | |
| 7 | 8.4/3.8/5 | 2 4/3 4 | |
| 8 | 6.4/3.12/7 | 2 3 6/5 | |
| 9 | 12.6/5.12/7 | 3 6/5 6 | |
| 10 | 4.8/5.8/5 | 2 4 | 4/3 |
| 11 | 12/5.12/5.3/2 | 2 3 | 6/5 |
| 12 | 4.4.3/2.3/2.3/2 | невитхоффова |
| 13 | 4.3/2.4.3/2.3/2 | | 2 4/3 4/3 (плосконосая) |
| 14 | 3.4.3.4/3.3.∞ | | 4/3 4 ∞ (плосконосая) |
Самодвойственные мозаики
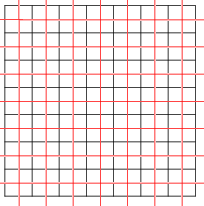
Мозаики могут быть самодвойственными. Квадратный паркет с символом Шлефли {4,4} является самодвойственным. На рисунке показаны два квадратных паркета (красный и чёрный), двойственных друг другу.
См. также
- Символ Витхоффа[англ.]
- Список однородных мозаик[англ.]
- Однородные мозаики на гиперболической плоскости
- Однородный многогранник
Примечания
Литература
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Grünbaum, Branko, G.C. Shephard. Tilings and Patterns (неопр.). — W. H. Freeman and Company[англ.], 1987. — ISBN 0-7167-1193-1. (Star tilings section 12.3)
- H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401–50 JSTOR: [1] (Table 8)
Ссылки
- Weisstein, Eric W. Uniform tessellation (англ.) на сайте Wolfram MathWorld.
- Uniform Tessellations on the Euclid plane Архивная копия от 4 июня 2016 на Wayback Machine
- Tessellations of the Plane Архивная копия от 24 февраля 2020 на Wayback Machine
- David Bailey's World of Tessellations Архивная копия от 2 апреля 2016 на Wayback Machine
- k-uniform tilings
- n-uniform tilings Архивная копия от 21 мая 2016 на Wayback Machine
- Richard Klitzing, 4D, Euclidean tilings Архивная копия от 4 марта 2016 на Wayback Machine