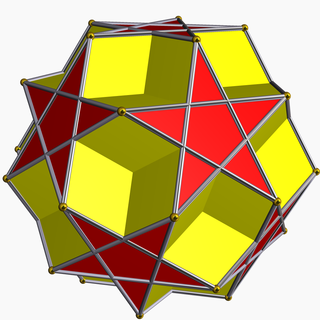
Однородный звёздчатый многогранник

Перейти к навигацииПерейти к поиску
Витрина с однородными многогранниками в Музее науки в Лондоне
Малый плосконосый икосоикосододекаэдр[англ.] является однородным звёздчатым многогранником с вершинной фигурой 35.5/2

Однородный звёздчатый многогранник — самопересекающийся однородный многогранник. Эти многогранники называются также невыпуклыми многогранниками, подчёркивая самопересечение. Каждый многогранник может содержать грани в виде звёздчатых многоугольников или иметь звёздчатые вершинные фигуры, но может содержать и то, и другое.

Полный набор 57 непризматических однородных звёздчатых многогранников включает 4 правильных, называемых телами Кеплера — Пуансо, 5 квазиправильных, и 48 полуправильных.

Существует также два бесконечных множества однородных звёздчатых призм и антипризм.

Так же, как (невырожденные) звёздчатые многоугольники (которые имеют плотность[англ.] большую 1) соответствуют круговым многоугольникам с перекрывающимися частями, звёздчатые многогранники, которые не проходят через центр, имеют плотность[англ.], большую 1, и соответствуют сферическим многогранникам с перекрывающимися частями. Существует 48 таких непризматических однородных звёздчатых многогранников. Оставшиеся 9 непризматических однородных звёздчатых многогранников имеют грани, проходящие через центр, являются полумногогранниками[англ.] и не соответствуют сферическим многогранникам, поскольку центр не может быть однозначно спроецирован на сферу.

Невыпуклые формы конструируются из треугольников Шварца.

Все треугольники, перечисленные ниже, сгруппированы по их группам симметрии, а внутри сгруппированы по расположению вершин.

Правильные многогранники помечены их символами Шлефли. Другие, неправильные однородные многогранники снабжены их вершинной конфигурацией или их номером однородного многогранника (Uniform polyhedron index, U(1-80)).

Примечание: Для невыпуклых форм ниже приводится дополнительное описание Неоднородный, когда выпуклая оболочка набора вершин[англ.] имеет ту же топологию, но имеет неправильные грани. Например, неоднородное скашивание (удаление рёбер) может дать прямоугольники на местах удалённых рёбер, а не квадраты.

Диэдральная симметрия

См. Призматический однородный многогранник.

Тетраэдральная симметрия

Треугольники (3 3 2) на сфере

Существует один невыпуклый вид, тетрагемигексаэдр, который имеет тетраэдральную симметрию (с фундаментальной областью треугольник Мёбиуса (3 3 2)).

Существует два треугольника Шварца, из которых образуются уникальные невыпуклые однородные многогранники — прямоугольный треугольник (3/2 3 2) и один треугольник общего вида (3/2 3 3). Треугольник (3/2 3 3) генерирует октагемиоктаэдр[англ.], который приведён ниже в разделе октаэдральной симметрии[англ.].

Расположение вершин[англ.]
(Выпуклая оболочка) 		Невыпуклые виды

Тетраэдр		 

Спрямлённый тетраэдр
Октаэдр
(4.3/2.4.3)
3/2 3 | 2

Усечённый тетраэдр		 

Скошенный тетраэдр
(Кубооктаэдр) 		 

Всеусечённый тетраэдр
(Усечённый октаэдр) 		 

Плосконосый тетраэдр
(Икосаэдр) 		 

Октаэдральная симметрия

Треугольники (4 3 2) на сфере

Существует 8 выпуклых форм и 10 невыпуклых с октаэдральной симметрией[англ.] (с фундаментальной областью треугольник Мёбиуса (4 3 2)).

Существует четыре треугольника Шварца, которые образуют невыпуклые формы, два прямоугольных, (3/2 4 2) и (4/3 3 2), и два общего вида, (4/3 4 3) и (3/2 4 4).

Расположение вершин[англ.]
(Выпуклая оболочка) 		Невыпуклые виды

Куб		 

Октаэдр		 

Кубооктаэдр
(6.4/3.6.4)[англ.]
4/3 4 | 3
(6.3/2.6.3)[англ.]
3/2 3 | 3

Усечённый куб
4.8/3.4/3.8/5)
 2 4/3 (3/2 4/2)  |
(8/3.3.8/3.4)[англ.]
3 4 | 4/3
(4.3/2.4.4)[англ.]
3/2 4 | 2

Усечённый октаэдр		 

Ромбокубооктаэдр
(4.8.4/3.8)[англ.]
2 4 (3/2 4/2) |
(8.3/2.8.4)[англ.]
3/2 4 | 4
(8/3.8/3.3)[англ.]
2 3 | 4/3

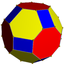Неоднородный
Усечённый кубооктаэдр
(4.6.8/3)[англ.]
2 3 4/3 |

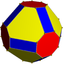Неоднородный
Усечённый кубооктаэдр
(8/3.6.8)[англ.]
3 4 4/3 |

Плосконосый куб 		 

Икосаэдральная симметрия

Треугольники (5 3 2) на сфере

Имеется 8 выпуклых форми и 46 невыпуклых с икосаэдральной симметрией (с фундаментальной областью треугольник Мёбиуса (5 3 2)). (или 47 невыпуклых форм, если включать фигуру Скиллинга). Некоторые невыпуклые плосконосые виды имеют зеркальную вершинную симметрию.

Расположение вершин[англ.]
(Выпуклая оболочка) 		Невыпуклые виды

Икосаэдр
{5,5/2}
{5/2,5}
{3,5/2}

Неоднородный
Усечённый икосаэдр
2 5 |3
U37[англ.]
2 5/2 | 5
U61[англ.]
5/2 3 | 5/3
U67[англ.]
5/3 3 | 2
U73[англ.]
2 5/3 (3/2 5/4) |

Неоднородный
Усечённый икосаэдр
2 5 |3
U38[англ.]
5/2 5 | 2
U44[англ.]
5/3 5 | 3
U56[англ.]
2 3 (5/4 5/2) |

Неоднородный
Усечённый икосаэдр
2 5 |3
U32[англ.]
| 5/2 3 3

Икосододекаэдр
2 | 3 5
U49[англ.]
3/2 3 | 5
U51[англ.]
5/4 5 | 5
U54
2 | 3 5/2
U70[англ.]
5/3 5/2 | 5/3
U71[англ.]
3 3 | 5/3
U36
2 | 5 5/2
U62[англ.]
5/3 5/2 | 3
U65[англ.]
5/4 5 | 3

Усечённый додекаэдр
2 3 | 5
U42[англ.]
U48[англ.]
U63[англ.]

Неоднородный
усечённый додекаэдр
U72[англ.]

Додекаэдр
{5/2,3}
U30[англ.]
U41[англ.]
U47[англ.]

Ромбоикосододекаэдр
U33[англ.]
U39[англ.]
U58[англ.]

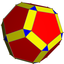Додекаэдр
со снятыми кромками
U55[англ.]

Неоднородный
Ромбоикосододекаэдр
U31[англ.]
U43[англ.]
U50[англ.]
U66[англ.]

Неоднородный
ромбоикосододекаэдр
U75[англ.]
U64[англ.]
Тело Скиллинга[англ.]
(см. ниже)

Неоднородный
Ромбоусечённый икосододекаэдр
U45[англ.]

Неоднородный
Ромбоусечённый икосододекаэдр
U59[англ.]

Неоднородный
Ромбоусечённый икосододекаэдр
U68[англ.]

Неоднородный
Плосконосый додекаэдр
U40[англ.]
U46[англ.]
U57[англ.]
U69
U60[англ.]
U74

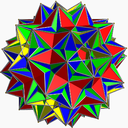
Тело Скиллинга

Ещё одним невыпуклым многогранником является большой биплосконосый биромбододекаэдр[англ.], известный также как тело Скиллинга, которое вершинно однородно, но имеет разделяемые общие для граней пары рёбер, так что четыре грани имеют одно общее ребро. Иногда его причисляют к однородным многогранникам, но не всегда. Тело имеет симметрию Ih.

Вырожденные случаи

Коксетер с помощью построения Витхоффа определил некоторое число вырожденных звёздчатых многогранников, которые имеют перекрывающиеся рёбра или вершины. Эти вырожденные формы включают:

  • Малый составной икосододекаэдр[англ.]
  • Большой составной икосододекаэдр[англ.]
  • Малый составной ромбоикосододекаэдр[англ.]
  • Составной ромбододекододекаэдр[англ.]
  • Большой составной ромбоикосододекаэдр[англ.]

См. также

Примечания

Литература

  • H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, вып. 916. — С. 401–450. — ISSN 0080-4614. — doi:10.1098/rsta.1954.0003. — JSTOR 91532.
  • М. Веннинджер. Модели многогранников. — «Мир», 1974.
  • M. Brückner. Vielecke und vielflache. Theorie und geschichte. — Leipzig, Germany: Teubner, 1900.
  • С.П. Сопов. Доказательство полноты перечня элементарных однородных многогранников // Украинский геометрический сборник. — 1970. — Вып. 8. — С. 139–156.
  • J. Skilling. The complete set of uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — 1975. — Т. 278. — С. 111–135. — ISSN 0080-4614. — doi:10.1098/rsta.1975.0022. — JSTOR 74475.
  • Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images
  • R. E. Mäder. Uniform Polyhedra // Mathematica. — 1993. — Вып. 3. — С. 48-57. [1] Архивная копия от 7 сентября 2015 на Wayback Machine
  • Peter W. Messer. Closed-Form Expressions for Uniform Polyhedra and Their Duals // Discrete & Computational Geometry. — 2002. — Вып. 27. — С. 353-375.
  • Richard Klitzing, 3D, uniform polyhedra Архивная копия от 23 октября 2015 на Wayback Machine

Ссылки